Basit kelimelerde toplam akım kanunu
Elektrik Mühendisliği adı verilen tanıdık bir konu, programında manyetik alan için fiziksel etkileşim ilkelerini tanımlayan bir dizi temel yasa içermektedir. Etkilerini elektrikli cihazların çeşitli unsurlarına, yapılarına ve ortamlarına genişletirler. İçlerinde meydana gelen süreçlerin fiziği, elektrik ve alan akımları gibi temel kavramlarla ilgilidir. Toplam akım yasası, elektrik yüklerinin hareketi ile yarattığı manyetik alan (daha kesin olarak, yoğunluğu) arasındaki ilişkiyi kurar. Modern bilim, uygulamasının neredeyse tüm ortamlara yayıldığını iddia ediyor.
Yasanın özü
Manyetik devrelerde geçerli kabul edilen yasa, kurucu bileşenleri arasında aşağıdaki nicel ilişkiyi belirler. Manyetik alan vektörünün kapalı bir döngüde dolaşımı, ona nüfuz eden akımların toplamı ile orantılıdır. Toplam akım yasasının fiziksel anlamını anlamak için, kendisinin tanımladığı süreçlerin grafiksel gösterimini tanımanız gerekir.
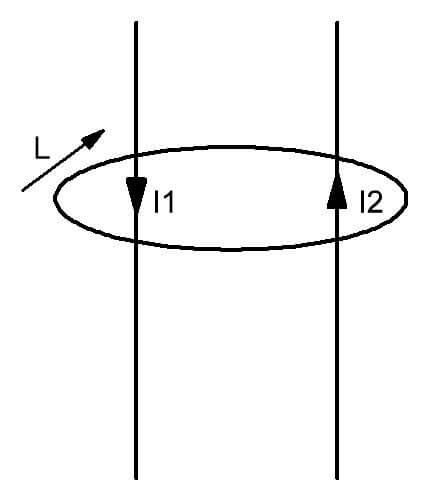
Şekillerden I1 ve I2 akımları olan yaklaşık iki iletkenin içinden aktığı yaklaşık olarak L devresi ile sınırlı bir alan oluşturulduğu, düzlemi hareketli yüklere sahip iletkenler tarafından delinmiş zihinsel olarak hayal edilen bir kapalı şekil olarak tanıtıldı. Basit bir ifadeyle, bu yasa aşağıdaki gibi ifade edilebilir. Kontur L tarafından kapsanan hayali hayali yüzey boyunca birkaç elektrik akışının varlığında, içinde önceden belirlenmiş bir yoğunluk dağılımına sahip bir manyetik alan oluşur.
Vektörün pozitif yönü için manyetik devrenin konturu yasasına uygun olarak saat yönünde seçilir. Ayrıca hayal edilebilir.
Akımlar tarafından oluşturulan girdap alanının böyle bir tanımı, akımların her birinin yönünün keyfi olabileceğini düşündürmektedir.
Referans için! Girilen alan yapısı ve onu tarif eden cihaz, her zaman devrenin baypas edilmesine eşit olan elektrostatik vektörün "E" dolaşımından ayırt edilmelidir. Bunun bir sonucu olarak, böyle bir alan potansiyel yapıları ifade eder. Manyetik alanın “B” vektörünün dolaşımı asla sıfır değildir. Bu yüzden buna “girdap” denir.
Temel konseptler
Söz konusu yasaya göre, manyetik alanları hesaplamak için aşağıdaki basitleştirilmiş yaklaşım kullanılmaktadır. Toplam akım, kapalı bir devre L ile kaplanan bir yüzeyden akan birkaç bileşenin toplamı olarak temsil edilir. Teorik hesaplamalar aşağıdaki gibi temsil edilebilir:
- Σ I devrelerinden akan toplam elektrik akımı, I1 ve I2'nin vektör toplamıdır.
- Bu örnekte, belirlemek için formülü kullanın:
ΣI = I1 - I2 (ikinci terimden önce eksi akımların yönünün ters olduğu anlamına gelir). - Bunlar, elektrik mühendisliğinde bilinen yasaya göre belirlenir (kural) burgu.
Kontur boyunca manyetik alan, özel tekniklerle elde edilen hesaplamalar temelinde hesaplanır. Bunu bulmak için, formlardan birinde sunulan Maxwell denklemini kullanarak bu parametreyi L üzerine entegre etmek gerekir.Diferansiyel formda uygulanabilir, ancak bu hesaplamaları biraz karmaşıklaştıracaktır.
Basitleştirilmiş Entegre Yaklaşım
Diferansiyel temsili kullanırsak, toplam akım yasasını basitleştirilmiş bir biçimde ifade etmek çok zor olacaktır (bu durumda, ek bileşenler içine dahil edilmelidir). Buna, devrenin içinde hareket eden akımlar tarafından oluşturulan manyetik girdap alanının, bu durumda, elektrik indüksiyonunun değişim oranına bağlı olan önyargı akımı dikkate alınarak belirlendiğini ekliyoruz.
Bu nedenle, pratikte, TOE'de, içinde oluşturulan girdap alanları olan bir devrenin mikroskobik olarak küçük segmentlerinin bir toplamı şeklinde tam akımlar için formüllerin sunumu daha popülerdir. Bu yaklaşım Maxwell denkleminin integral formda uygulanmasını içerir. Uygulandığında, kontur, ilk yaklaşımda doğrudan olduğu düşünülen küçük bölümlere ayrılır (yasaya göre manyetik alanın homojen olduğu varsayılır). Vakumda hareket eden manyetik alanın ΔL uzunluğunun ayrı bir kesiti için Um olarak belirtilen bu değer aşağıdaki gibi tanımlanır:
Um = HL * ΔL
Kısaca integral formda sunulan tam kontur L boyunca toplam gerilim aşağıdaki formülle bulunur:
UL = Σ HL * ΔL.
Vakum için toplam akım kanunu
Bütünleşme kurallarına göre hazırlanan son haliyle, toplam akım yasası şuna benzer. "B" vektörünün kapalı bir döngü içinde dolaşımı manyetik sabitin ürünü olarak gösterilebilir m akım miktarında:
B'nin dL üzerinden integrali = Bl'nin dL üzerinden integrali = m Σ Giriş
burada n, keyfi olarak zihinsel olarak hayal edilen bir devre L tarafından kapsanan çok yönlü akımlara sahip toplam iletken sayısıdır.
Her bir akım, bu formülde tamamen bu devre tarafından kaplandığı kadar dikkate alınır.
Toplam akım yasası için elde edilen hesaplamaların nihai formu, indüklenen elektromanyetik kuvvetin (alan) hareket ettiği ortamdan büyük ölçüde etkilenir.
Çevresel Etki
Bir boşlukta değil, manyetik bir ortamda hareket eden akımlar ve alanlar için dikkate alınan ilişkiler biraz farklı bir form alır. Bu durumda, ana akım bileşenlerine ek olarak, örneğin bir mıknatısta veya buna benzer herhangi bir malzemede ortaya çıkan mikroskobik akımlar kavramı ortaya çıkar.
Gerekli ilişki, manyetik indüksiyon B'nin vektör sirkülasyonu teoreminden tam olarak türetilmiştir. Basit bir şekilde, aşağıdaki formda ifade edilir. Seçilen devre üzerine entegre edildiğinde B vektörünün toplam değeri, kapladığı makro akımlarının toplamına, manyetik sabitin katsayısı ile çarpılır.
Sonuç olarak, bir maddede "B" formülü şu ifadeyle belirlenir:
B'nin dL üzerinden integrali = Bl'nin dL üzerinden integrali = m(ben+ben1)
burada: dL, bypass boyunca yönlendirilen devrenin ayrık elemanıdır, Bl, keyfi bir noktada tanjant yönündeki bileşendir, bI ve I1, iletim akımı ve mikroskopik (moleküler) akımdır.
Alan keyfi malzemelerden oluşan bir ortamda hareket ediyorsa, bu yapıların karakteristik mikroskobik akımları dikkate alınmalıdır.
Bu hesaplamalar, solenoidde veya sonlu manyetik geçirgenliğe sahip herhangi bir başka ortamda oluşturulan alan için de geçerlidir.
Referans için
GHS'nin en eksiksiz ve kapsamlı ölçüm sisteminde, manyetik alan kuvveti Oersteds (E) 'de temsil edilir. Mevcut başka bir sistemde (SI) metre başına amper (A / metre) olarak ifade edilir. Bugün, oersted yavaş yavaş daha uygun bir ünite ile değiştiriliyor - metre başına bir amper.Ölçümlerin veya hesaplamaların sonuçlarını SI'dan GHS'ye çevirirken aşağıdaki oran kullanılır:
1 e = 1000 / (4π) A / m ≈ 79.5775 amper / metre.
İncelemenin son bölümünde, tam akımlar yasasının ifadesi ne olursa olsun, özünün değişmeden kaldığını not ediyoruz. Kendi sözleriyle, bu şu şekilde temsil edilebilir: bu devreye giren akımlar ile maddede oluşturulan manyetik alanlar arasındaki ilişkiyi ifade eder.
Son olarak, makalenin konusuyla ilgili faydalı bir video izlemenizi öneririz:
İlgili malzemeler: