Kirchhoff'un Birinci ve İkinci Yasaları - Uygun Bir Açıklama
Kirchhoff'un birinci yasası
Birinci yasanın tanımı: “Bir düğümden akan akımların cebirsel toplamı sıfırdır. ” Biraz farklı bir form söyleyebilirsiniz: "Düğüme kaç akım aktı, aynı sayı aktı, bu da akımın sabitliğini gösteriyor ”.
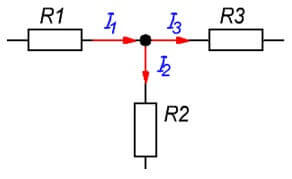
Bir zincirin düğümü, üç veya daha fazla dalın bağlantı noktasıdır. Bu durumda akımlar, her dalın direnci ile orantılı olarak dağıtılır.
ben1= Ben2+ I3
Bu kayıt şekli DC devreleri için geçerlidir. Alternatif bir akım devresi için ilk Kirchhoff yasasını kullanırsanız, anlık voltaj değerleri kullanılır, İ harfi ile gösterilir ve karmaşık biçimde yazılır ve hesaplama yöntemi aynı kalır:
Karmaşık form hem aktif hem de reaktif bileşenleri dikkate alır.
Kirchhoff'un İkinci Kanunu
Birincisi dallardaki akımların dağılımını açıklarsa, ikinci Kirchhoff yasası: “Devredeki voltaj düşüşlerinin toplamı tüm EMF'lerin toplamına eşittir. ”Basit bir ifadeyle, ifadeler şu şekildedir: “Bir devrenin bir bölümüne uygulanan EMF, bu devrenin elemanları arasında dirençlerle orantılı olarak dağıtılacaktır, yani. Ohm yasasına göre. "
Alternatif akım için şöyle geliyor: “Kompleks EMF'nin genliklerinin toplamı, elemanlardaki karmaşık voltaj düşüşlerinin toplamına eşittir ".
Z toplam direnç veya karmaşık dirençtir, hem dirençli hem de alternatif akımın frekansına bağlı reaktif (endüktans ve kapasitans) içerir (doğru akımda sadece aktif direnç vardır). Aşağıda kapasitörün ve endüktansın karmaşık direncinin formülleri vardır:
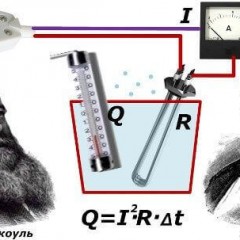
Yukarıdakileri gösteren bir resim:
Sonra:
Kirchhoff'un birinci ve ikinci yasaları için hesaplama yöntemleri
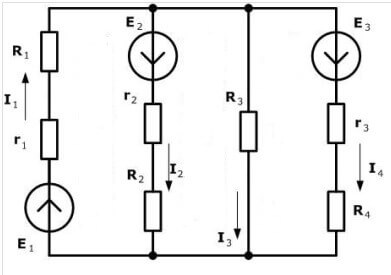
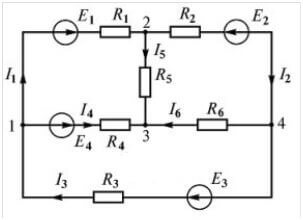
Teorik materyali uygulamaya koyalım. İşaretleri denklemlere doğru bir şekilde yerleştirmek için devrenin yönünü seçmeniz gerekir. Şemaya bir göz atın:
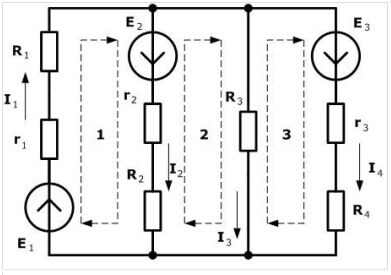
Saat yönünde bir yön seçmenizi ve şekilde işaretlemenizi öneririz:
Kesik noktalı çizgi, denklemler oluştururken yolun nasıl izleneceğini gösterir.
Bir sonraki adım Kirchhoff yasalarına göre denklemler oluşturmaktır. Önce ikincisini kullanıyoruz.İşaretleri şöyle koyarız: saat yönünün tersine (önceki adımda seçtiğimiz yön) yönlendirilirse elektromotor kuvvetin önüne bir eksi işareti yerleştirilir, sonra saat yönünde emf için bir eksi işareti koyarız. İşaretleri dikkate alarak her devre için oluşturuyoruz.
Birincisi, EMF'nin yönüne bakıyoruz, E1 artı E2'yi ayarlayan kesik çizgili çizgiyle çakışıyor:
İkincisi için:
Üçüncüsü için:
IR (voltaj) işaretleri döngü akımlarının yönüne bağlıdır. Burada işaret kuralı bir önceki durumda olduğu gibidir.
Eğer akım devre bypass yönü yönünde akıyorsa IR pozitif bir işaret ile yazılır. Ve eğer akım devrenin yönüne doğru akıyorsa, “-” işareti ile.
Devre geçişinin yönü koşullu bir miktardır. Sadece denklemlerdeki işaretlerin düzenlenmesi için gereklidir, keyfi olarak seçilir ve hesaplamaların doğruluğunu etkilemez. Bazı durumlarda, kötü seçilmiş bir baypas yönü hesaplamayı zorlaştırabilir, ancak bu kritik değildir.
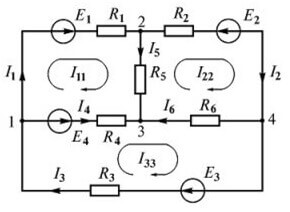
Başka bir devre düşünün:
Dört kadar EMF kaynağı vardır, ancak hesaplama prosedürü aynıdır, önce denklemleri yapmak için yönü seçiyoruz.
Şimdi Kirchhoff'un birinci yasasına göre denklemler yapmanız gerekiyor. İlk düğüm için (diyagramın solundaki şekil 1):
ben3 içeri akar ve ben1, Ben4 izler, dolayısıyla işaretler. İkincisi için:
Üçüncüsü için:
Soru: "Dört düğüm var ve sadece üç denklem var, neden? ”Gerçek şu ki, ilk Kirchhoff kuralının denklemlerinin sayısı eşittir:
N-denklemler= nknot-1
yani düğümlerden sadece 1 daha az denklem vardır, çünkü bu, tüm dallardaki akımları tanımlamak için yeterlidir, bir kez daha devreye gitmenizi ve tüm akımların denklemlere yazılıp yazılmadığını kontrol etmenizi öneririm.
Şimdi ikinci kurala göre denklemlerin inşasına geçiyoruz. Birincil devre için:
İkinci devre için:
Üçüncü devre için:
Gerçek voltaj ve direnç değerlerini değiştirirsek, o zaman birinci ve ikinci yasaların adil ve yerine getirildiği ortaya çıkar. Bunlar basit örneklerdir; pratikte çok daha hacimli problemlerin çözülmesi gerekir.
Sonuç. Birinci ve ikinci Kirchhoff yasalarının yardımıyla hesaplarken ana şey, denklem yapma kuralının gözetilmesidir, yani. devrenin her elemanı için işaretlerin doğru düzenlenmesi için akım akışının ve devre baypasının yönünü dikkate alın.
Kirchhoff'un manyetik devre yasaları
Manyetik devrelerin hesaplamaları elektrik mühendisliğinde de önemlidir, her iki yasa da burada uygulamalarını bulmuştur. Öz aynı kalır, ancak tür ve boyut değişir, bu konuya daha ayrıntılı olarak bakalım. İlk önce kavramlarla uğraşmanız gerekir.
Manyetomotive kuvvet (MDS), bobinin dönüş sayısının, içinden geçen akımın çarpımı ile belirlenir:
F = w * i
Manyetik voltaj, Amper cinsinden ölçülen bir bölüm boyunca manyetik alan kuvveti ve akımının ürünüdür:
Um= H * I
Veya manyetik direnç yoluyla manyetik akı:
Um= F * Rm
L çizimin ortalama uzunluğu, μr ve μ0 - bağıl ve mutlak manyetik geçirgenlik.
Bir benzetme yaparak, manyetik bir devre için ilk Kirchhoff yasasını yazıyoruz:
Yani, düğümden geçen tüm manyetik akıların toplamı sıfırdır. Seslerin neredeyse bir elektrik devresi ile aynı olduğunu fark ettiniz mi?
Sonra Kirchhoff'un ikinci yasası şöyle geliyor: “Manyetik devredeki MDS toplamı U toplamına eşittir.M (manyetik stres).
Manyetik akı şuna eşittir:
Alternatif bir manyetik alan için:
Manyetik devrenin parametrelerine değil, yalnızca sarımdaki voltaja bağlıdır.
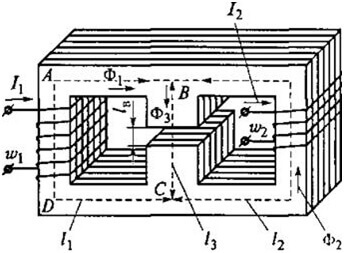
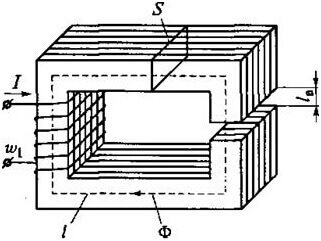
Örnek olarak, bu konturu düşünün:
Sonra ABCD için aşağıdaki formülü elde ederiz:
Hava boşluğu olan devreler için aşağıdaki ilişkiler doğrudur:
Manyetik Direnç:
Ve hava boşluğunun direnci (çekirdeğin sağında):
Burada S çekirdek alandır.
Materyali tam olarak anlamak ve kuralları kullanmanın bazı nüanslarını görsel olarak gözden geçirmek için videoda verilen dersleri öğrenmenizi öneririz:
Gustav Kirchhoff'un keşifleri bilimin, özellikle elektrik mühendisliğinin gelişmesine önemli bir katkıda bulundu.Onların yardımı ile, herhangi bir elektrik veya manyetik devreyi, içindeki akımları ve voltajları hesaplamak oldukça basittir. Artık Kirchhoff’un elektrik ve manyetik devreler için kurallarının size daha açık hale geleceğini umuyoruz.
Benzer malzemeler:

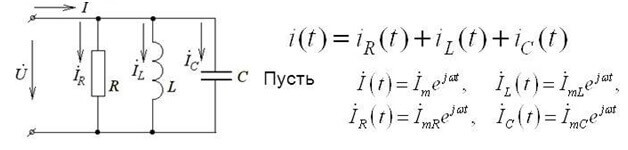
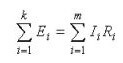
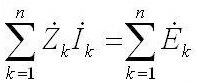
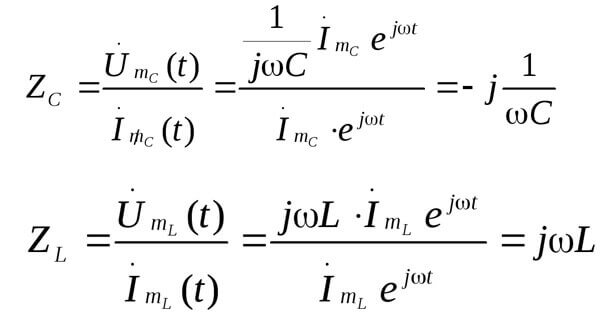

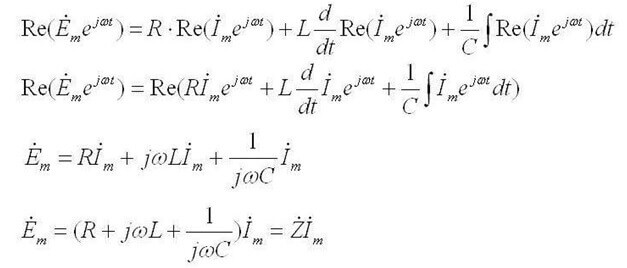
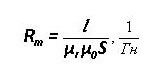
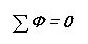
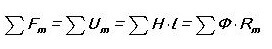
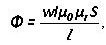
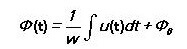
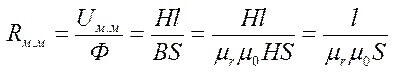
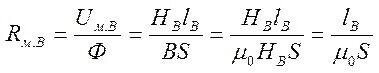


Kirchhoff'un birinci yasasına göre ur'nizi oluşturduğumuzda, yani ilk urun iyi bir açıklaması. Neden her şey çok daha bariz olduğunda ikinci ve üçüncü için bir açıklama yok? I2 açıkça oraya akıyor, ama nedense olumlu bir işareti var
üçüncü denklemde, genelde üç ben de içeri giriyorum. Neden olumlular?
Makalenin başında denklemin I1 = I2 + I3 biçiminde kabul edildiğini, eğer her şeyi denklemin sol tarafına aktarırsanız, I1-I2-I3 = 0 olduğunu lütfen unutmayın. Aynı şey orada yapıldı.
İkinci düğüm için:
I1 = I5 + I2
her şeyi bir yönde hareket ettirmek ortaya çıkacaktır:
I1-I5-I2 = 0
Devre bypassının yönü ile karşılaştırıldığında, işaretleri değiştirmenin daha iyi olduğu, yani eksi 1 ile çarpıldığı anlaşılmaktadır.
Çıkacak
-I1 + I5 + I2 = 0
eşdeğer
I2 + I5-I1 = 0