Loven om total strøm i enkle ord
Faget kjent for mange, med tittelen “Elektroteknikk”, inneholder i sitt program en serie grunnleggende lover som definerer prinsippene for fysisk samhandling for et magnetfelt. De utvider effekten til forskjellige elementer av elektriske apparater, så vel som deres strukturer og miljøer. Fysikken i prosessene som forekommer i dem forholder seg til slike grunnleggende konsepter som strøm av strøm og felt. Loven om den totale strømmen fastsetter forholdet mellom bevegelsen av elektriske ladninger og magnetfeltet som er opprettet av den (mer presist, dens intensitet). Moderne vitenskap hevder at bruken av den strekker seg til nesten alle miljøer.
Lovens essens
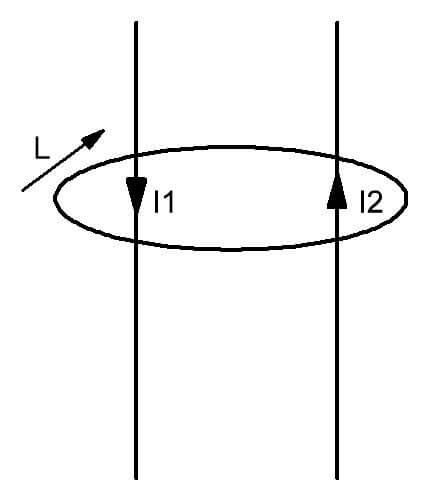
Den betraktede loven som gjelder i magnetiske kretsløp, bestemmer følgende kvantitative forhold mellom dets bestanddeler. Sirkulasjonen av magnetfeltvektoren i en lukket sløyfe er proporsjonal med summen av strømningene som trenger inn i den. For å forstå den fysiske betydningen av loven om total strøm, må du gjøre deg kjent med den grafiske fremstillingen av prosessene beskrevet av ham.
Det fremgår av figuren at omtrent to ledere med strømmer I1 og I2 som strømmer gjennom dem, et felt dannes, begrenset av kretsen L. Det er introdusert som en mentalt innbilt lukket figur, hvis plan er gjennomboret av ledere med bevegelige ladninger. Med enkle ord kan denne loven uttrykkes som følger. I nærvær av flere strømmer av elektrisitet gjennom den tenkelige imaginære overflaten dekket av kretsen L, dannes et magnetfelt med en gitt spenningsfordeling inne i den.
For den positive retningen til vektoren i samsvar med loven for konturen av magnetkretsen velges med klokken. Det er også tenkelig.
En slik definisjon av virvelfeltet opprettet av strømningene antyder at retningen til hver av strømningene kan være vilkårlig.
For referanse! Den innførte feltstrukturen og apparatet som beskriver det, bør skilles fra sirkulasjonen av den elektrostatiske vektoren "E", som alltid er lik null ved å omgå kretsen. Som et resultat av dette refererer et slikt felt til potensielle strukturer. Sirkulasjonen av vektoren "B" i magnetfeltet er aldri null. Derfor kalles det en "virvel".
Grunnleggende konsepter
I samsvar med loven som behandles brukes følgende forenklede tilnærming for å beregne magnetiske felt. Den totale strømmen er representert som summen av flere komponenter som strømmer gjennom en overflate dekket av en lukket krets L. Teoretiske beregninger kan representeres som følger:
- Den totale elektriske strømmen som strømmer gjennom kretsene Σ I er vektorsummen av I1 og I2.
- For å bestemme det i dette eksemplet, bruk formelen:
ΣI = I1 - I2 (minus før andre termin betyr at gjeldende retninger er motsatt). - De blir på sin side bestemt i henhold til loven kjent i elektroteknikk (regel) gimlet.
Magnetfeltet langs konturen beregnes på grunnlag av beregningene oppnådd ved spesielle teknikker. For å finne det, er det nødvendig å integrere denne parameteren over L ved å bruke Maxwell-ligningen som er presentert i en av skjemaene.Det kan brukes i differensialform, men dette vil komplisere beregningene noe.
Forenklet integrert tilnærming
Hvis vi bruker differensialrepresentasjonen, vil det å uttrykke loven for den totale strømmen i en forenklet form være veldig vanskelig (i dette tilfellet må ytterligere komponenter innføres i den). Vi legger til dette at det magnetiske virvelfeltet som skapes av strømningene som beveger seg innenfor kretsen, bestemmes i dette tilfellet under hensyntagen til forspenningsstrømmen, som avhenger av endringshastigheten for elektrisk induksjon.
Derfor, i praksis, i TOE, er presentasjonen av formler for fullstrømmer i form av en summering av mikroskopisk små segmenter av en krets med virvelfelt opprettet i dem mer populær. Denne tilnærmingen innebærer anvendelse av Maxwell-ligningen i integrert form. Når den implementeres, deles konturen i små segmenter, som anses å være greie i den første tilnærmingen (i henhold til loven antas det at magnetfeltet er homogent). Denne verdien, betegnet som Um for en diskret del av lengden ΔL på magnetfeltet som virker i vakuum, er definert som følger:
Um = HL * ΔL
Den totale spenningen langs hele konturen L, presentert kort i integrert form, blir funnet ved følgende formel:
UL = Σ HL * ΔL.
Loven for den totale strømmen for vakuum
I sin endelige form, utarbeidet i henhold til alle integreringsregler, ser loven om total strøm ut slik. Sirkulasjon av vektoren "B" i en lukket sløyfe kan representeres som produktet av den magnetiske konstanten m i mengden strømmer:
Integralet av B over dL = integralet av Bl over dL = m Σ Inn
hvor n er det totale antall ledere med multidireksjonsstrømmer dekket av en mentalt innbilt krets L av vilkårlig form.
Hver strøm tas i betraktning i denne formelen så mange ganger som den er fullstendig dekket av denne kretsen.
Det endelige synet på de oppnådde beregningene for loven om total strøm påvirkes sterkt av mediet der den induserte elektromagnetiske kraften (felt) virker.
Miljøpåvirkning
De betraktede forholdene for loven om strømmer og felt som ikke fungerer i et vakuum, men i et magnetisk medium, tar en litt annen form. I dette tilfellet, i tillegg til hovedstrømkomponentene, introduseres konseptet med mikroskopiske strømmer som oppstår i en magnet, for eksempel eller i noe lignende materiale.
Den nødvendige relasjonen avledes i sin helhet fra teoremet om vektorsirkulasjonen av magnetisk induksjon B. Enkelt uttrykt er det uttrykt i følgende form. Den totale verdien av vektoren B når den er integrert over den valgte kretsen, er lik summen av makrostrømmene dekket av den multiplisert med koeffisienten til magnetkonstanten.
Som et resultat bestemmes formelen for "B" i et stoff av uttrykket:
Integralet av B over dL = integralet av Bl over dL = m(jeg+jeg1)
hvor: dL er det diskrete elementet i kretsen rettet langs omløpet, Bl er komponenten i retningen til tangenten på et vilkårlig punkt, bI og I1 er ledningsstrømmen og den mikroskopiske (molekylære) strømmen.
Hvis feltet fungerer i et miljø som består av vilkårlige materialer, bør de mikroskopiske strømningene karakteristiske for disse strukturene tas med i betraktningen.
Disse beregningene gjelder også for feltet som er opprettet i magnetventilen eller i et hvilket som helst annet medium med endelig magnetisk permeabilitet.
For referanse
I det mest komplette og omfattende systemet med målinger av GHS er magnetfeltstyrken representert i Oersteds (E). I et annet eksisterende system (SI) er det uttrykt i ampere per meter (A / meter). I dag erstattes oersted gradvis av en mer praktisk enhet i drift - en ampere per meter.Når du oversetter resultatene av målinger eller beregninger fra SI til GHS, brukes følgende forhold:
1 E = 1000 / (4π) A / m ≈ 79,5775 Ampere / meter.
I den siste delen av gjennomgangen bemerker vi at uansett hva ordlyden i loven om fulle strømmer brukes, forblir essensen uendret. Med hans egne ord kan dette fremstilles som følger: det uttrykker forholdet mellom strømningene som trenger inn i denne kretsen og magnetfeltene som er opprettet i stoffet.
Til slutt anbefaler vi å se en nyttig video om artikkelen:
Relaterte materialer: