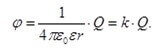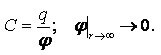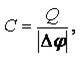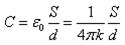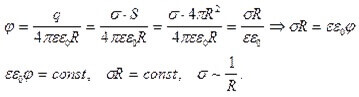Hvordan ladninger fordeles i en leder når strømmen strømmer
Ladebærere og deres bevegelse
En leder er et stoff der bærere begynner å bevege seg under påvirkning av det minste eksterne elektriske feltet. Når det ikke er noe eksternt felt, avbryter feltene positive ioner og negative elektroner hverandre. Vi undersøkte en relatert problemstilling mer detaljert og sammenlignet ledere, dielektrika og halvledere i en artikkel publisert tidligere.
Tenk på et metallgjenstand som er i et elektrisk felt. Ladeskipene begynner å bevege seg under påvirkning av et eksternt felt på grunn av det faktum at Coulomb-styrkene begynner å handle på ladningsbærerne. Dessuten ligger handlingsretningen til disse kreftene på positive og negative bærere i en annen retning. Bevegelsen stopper hvis summen av intensiteten til de ytre og indre felt blir null, det vil si:
Erez = E intern + E ekstern = 0
I dette tilfellet er feltstyrken lik:
E = dF / dt
Hvis spenningen er null, er potensialet i kroppen lik et konstant antall. Dette vil bli klart hvis vi uttrykker potensialet fra denne formelen og integrerer, det vil si:
Positive ioner og elektroner fra hele kroppens volum skynder seg til overflaten for å kompensere for spenningen elektrisk felt. Så inni lederen blir det elektriske feltet lik null, siden det er balansert av ladningsbærere fra overflaten.
Interessant! En overflate som det samme potensialet er til stede på alle punkter kalles ekvipotensiell.
Hvis vi vurderer dette problemet mer detaljert, når en leder blir introdusert i et elektrisk felt, beveger positive ioner seg mot feltlinjene og negative elektroner i samme retning. Dette skjer til de er fordelt, og feltet i lederen blir lik null. Slike kostnader kalles indusert eller overskytende.
Viktig! Når ladningene kommuniseres til ledende materiale, fordeles de slik at en likevektsstilstand oppnås. De samme ladningene vil avvise og tendere i samsvar med retningen på kraftlinjene til det elektriske feltet.
Det følger at arbeidet med å flytte ladningsbærere er null, noe som er lik potensialforskjellen. Da er potensialet i forskjellige deler av lederen lik et konstant antall og endres ikke.Det er viktig å vite at i et dielektrikum, for å rive av en ladningsbærer, for eksempel et elektron fra et atom, må store krefter påføres. Derfor blir de beskrevne fenomenene i generell forstand observert på ledende organer.
Elektrisk kapasitet på en enslig leder
Først bør du vurdere konseptet med en enslig leder. Dette er en leder som er fjernt fra andre ladede ledere og kropper. Dessuten vil potensialet på det avhenge av ladningen.
Den elektriske kapasiteten til en enslig leder er en leders evne til å holde en distribuert ladning. Aller først avhenger det av formen på lederen.
Hvis to slike legemer er atskilt med et dielektrikum, for eksempel luft, glimmer, papir, keramikk, etc. - få en kondensator. Kapasiteten avhenger av avstanden mellom platene og deres område, samt av potensialforskjellen mellom dem.
Formlene beskriver kapasitansens avhengighet av potensialforskjellen og de geometriske dimensjonene til en flat kondensator. Lære mer om hva er elektrisk kapasitet, kan du fra vår egen artikkel.
Ladefordeling og kroppsform
Så, distribusjonstettheten av ladningsbærere avhenger av formen til lederen. Tenk på dette med eksemplet med formler for en sfære.
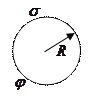
Anta at vi har en viss metallladet sfære, med radius R, ladetetthet på overflaten G og potensial F. Deretter:
Fra den sist avledede formelen kan vi forstå at tettheten er omvendt proporsjonal med sfærens radius.
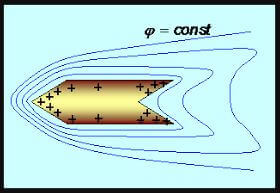
Det vil si at jo mer konveks og skarp gjenstanden er, jo større er tettheten av bærere på dette stedet. På konkave overflater er tettheten minimal. Dette kan sees i videoen:
Praktisk anvendelse
Hvis du tar hensyn til det ovennevnte, er det verdt å merke seg at strømmen strømmer gjennom kabelen og blir fordelt, som om rørets ytre diameter. Dette skyldes egenskapene til fordelingen av elektroner i et ledende legeme.
Det er underlig at når strøm flyter i systemer med høyfrekvent strøm, blir en hudeffekt observert. Dette er fordelingen av ladninger på overflaten av lederne. Men i dette tilfellet observeres et enda tynnere "ledende" lag.
Hva betyr det? Dette antyder at for strømmen av lik størrelse med en nettverksfrekvens på 50 Hz og en frekvens på 50 kHz i en høyfrekvenskrets, vil et større tverrsnitt av den ledende kjerne være nødvendig. I praksis observeres dette ved å bytte strømforsyning. Det er nettopp slike strømmer som flyter i transformatorene deres. For å øke tverrsnittsarealet, velg enten en tykk ledning eller vikling av viklingene med flere årer samtidig.
Avhengigheten av tetthetsfordelingen på overflateformen beskrevet i forrige seksjon brukes i praksis i lynbeskyttelsessystemer. Det er kjent at for å beskytte mot lynskader, er en av typene lynbeskyttelse installert, for eksempel en lynstav. På overflaten samles ladede partikler, på grunn av hvilken utslippet skjer nøyaktig i det, noe som igjen bekrefter det som ble sagt om deres distribusjon.
Til slutt anbefaler vi å se en video der den med enkle ord forklarer og tydelig viser hvordan anklagene er fordelt i dirigenten:
Dette er alt vi ønsket å fortelle deg om hvordan ladefordelingen i lederen skjer når strømmen strømmer. Vi håper at informasjonen som ble gitt, var forståelig og nyttig for deg!
Relaterte materialer: