De wet van totale stroom in eenvoudige woorden
Een bekend onderwerp, elektrotechniek genaamd, bevat in zijn programma een reeks fundamentele wetten die de principes van fysieke interactie voor een magnetisch veld definiëren. Ze breiden hun effect uit naar verschillende elementen van elektrische apparaten, evenals hun structuren en omgevingen. De fysica van de processen die daarin plaatsvinden, heeft betrekking op basisconcepten als stromen van elektriciteit en velden. De wet van de totale stroom legt de relatie vast tussen de beweging van elektrische ladingen en het daardoor opgewekte magnetische veld (meer bepaald de intensiteit). De moderne wetenschap beweert dat de toepassing ervan zich uitstrekt tot bijna alle omgevingen.
De essentie van de wet
De wet die van toepassing is op magnetische circuits bepaalt de volgende kwantitatieve relatie tussen de samenstellende componenten. De circulatie van de magnetische veldvector in een gesloten lus is evenredig met de som van de stromen die erin doordringen. Om de fysieke betekenis van de wet van totale stroom te begrijpen, moet u vertrouwd raken met de grafische weergave van de door hem beschreven processen.
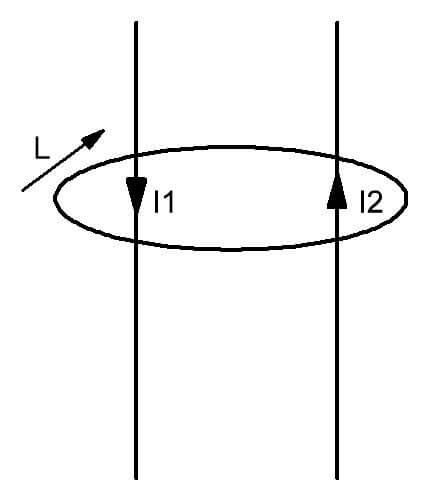
Uit de figuur blijkt dat ongeveer twee geleiders met stromen I1 en I2 erdoorheen stromen, een veld wordt gevormd, begrensd door het circuit L. Het wordt geïntroduceerd als een mentaal ingebeelde gesloten figuur, waarvan het vlak wordt doorboord door geleiders met bewegende ladingen. In eenvoudige woorden kan deze wet als volgt worden uitgedrukt. In aanwezigheid van meerdere stroomstromen door het denkbeeldige denkbeeldige oppervlak dat door het circuit L wordt bedekt, wordt daarin een magnetisch veld gevormd met een bepaalde spanningsverdeling.
Voor de positieve bewegingsrichting van de vector in overeenstemming met de wet voor de contour van het magnetische circuit wordt met de klok mee geselecteerd. Het is ook denkbaar.
Een dergelijke definitie van het door de stromingen gecreëerde wervelveld suggereert dat de richting van elk van de stromen willekeurig kan zijn.
Ter referentie! De geïntroduceerde veldstructuur en het apparaat dat het beschrijft, moeten worden onderscheiden van de circulatie van de elektrostatische vector "E", die altijd gelijk is aan nul en het circuit omzeilt. Als gevolg hiervan verwijst zo'n veld naar potentiële structuren. De circulatie van de vector “B” van het magnetische veld is nooit nul. Daarom wordt het een "vortex" genoemd.
Basisconcepten
Overeenkomstig de desbetreffende wet wordt de volgende vereenvoudigde benadering gebruikt om magnetische velden te berekenen. De totale stroom wordt weergegeven als de som van verschillende componenten die door een oppervlak stromen dat is bedekt met een gesloten circuit L. Theoretische berekeningen kunnen als volgt worden weergegeven:
- De totale elektrische stroom die door de circuits Σ I stroomt, is de vectorsom van I1 en I2.
- Gebruik in dit voorbeeld de formule om dit te bepalen:
ΣI = I1 - I2 (min voor de tweede term betekent dat de richtingen van stromen tegengesteld zijn). - Ze worden op hun beurt bepaald volgens de wet die bekend is in de elektrotechniek (regel) gimlet.
Het magnetische veld langs de contour wordt berekend op basis van de berekeningen verkregen met speciale technieken. Om het te vinden, moet deze parameter over L worden geïntegreerd met behulp van de Maxwell-vergelijking die in een van de vormen wordt gepresenteerd.Het kan in differentiële vorm worden toegepast, maar dit zal de berekeningen enigszins bemoeilijken.
Vereenvoudigde geïntegreerde aanpak
Als we de differentiële representatie gebruiken, zal het erg moeilijk zijn om de totale huidige wet in een vereenvoudigde vorm uit te drukken (in dit geval moeten er extra componenten in worden opgenomen). We voegen hieraan toe dat het magnetische vortexveld dat wordt gecreëerd door de stromen die binnen het circuit bewegen, in dit geval wordt bepaald rekening houdend met de instelstroom, die afhankelijk is van de veranderingssnelheid van elektrische inductie.
Daarom is in TOE in de praktijk de presentatie van formules voor volledige stromen in de vorm van optelling van microscopisch kleine segmenten van een circuit met daarin gecreëerde wervelvelden populairder. Deze benadering omvat de toepassing van de Maxwell-vergelijking in integrale vorm. Bij de implementatie wordt de contour verdeeld in kleine segmenten, die in de eerste benadering als rechtlijnig worden beschouwd (volgens de wet wordt aangenomen dat het magnetische veld homogeen is). Deze waarde, aangegeven als Um voor één discreet stuk lengte ΔL van het in vacuüm werkende magnetische veld, wordt als volgt gedefinieerd:
Um = HL * ΔL
De totale spanning langs de volledige contour L, kort weergegeven in integrale vorm, wordt gevonden met de volgende formule:
UL = Σ HL * ΔL.
De wet van de totale stroom voor vacuüm
In zijn uiteindelijke vorm, opgesteld volgens alle integratieregels, ziet de wet van de totale stroom er zo uit. Circulatie van de vector "B" in een gesloten lus kan worden gerepresenteerd als het product van de magnetische constante m in het aantal stromen:
De integraal van B over dL = de integraal van Bl over dL = m Σ In
waar n is het totale aantal geleiders met multidirectionele stromen bedekt door een mentaal ingebeelde schakeling L van willekeurige vorm.
Elke stroom wordt in deze formule even vaak in aanmerking genomen als volledig gedekt door dit circuit.
De uiteindelijke vorm van de verkregen berekeningen voor de wet van de totale stroom wordt sterk beïnvloed door het medium waarin de geïnduceerde elektromagnetische kracht (veld) inwerkt.
Milieu-impact
De overwogen relaties voor de wet van stromen en velden die niet in een vacuüm, maar in een magnetisch medium werken, krijgen een iets andere vorm. In dit geval wordt, naast de belangrijkste stroomcomponenten, het concept van microscopische stromen die bijvoorbeeld in een magneet of in een soortgelijk materiaal ontstaan, geïntroduceerd.
De noodzakelijke relatie is volledig afgeleid van de stelling over de vectorcirculatie van magnetische inductie B. In eenvoudige termen wordt het uitgedrukt in de volgende vorm. De totale waarde van de vector B wanneer geïntegreerd over het geselecteerde circuit is gelijk aan de som van de macrostromen die eronder vallen vermenigvuldigd met de coëfficiënt van de magnetische constante.
Als resultaat wordt de formule voor "B" in een stof bepaald door de uitdrukking:
De integraal van B over dL = de integraal van Bl over dL = m(Ik+Ik1)
waar: dL is het discrete element van het circuit dat langs zijn bypass is gericht, Bl is de component in de richting van de raaklijn op een willekeurig punt, bI en I1 zijn de geleidingsstroom en de microscopische (moleculaire) stroom.
Als het veld werkt in een omgeving die bestaat uit willekeurige materialen, moet er rekening worden gehouden met de microscopische stromen die kenmerkend zijn voor deze structuren.
Deze berekeningen gelden ook voor het veld dat in de solenoïde of in een ander medium met een eindige magnetische permeabiliteit is gecreëerd.
Ter referentie
In het meest complete en uitgebreide meetsysteem van GHS wordt de magnetische veldsterkte weergegeven in Oersteds (E). In een ander bestaand systeem (SI) wordt het uitgedrukt in ampère per meter (A / meter). Tegenwoordig wordt oersted geleidelijk vervangen door een handiger toestel in bedrijf - een ampère per meter.Bij het vertalen van de resultaten van metingen of berekeningen van SI naar GHS wordt de volgende verhouding gebruikt:
1 E = 1000 / (4π) A / m ≈ 79,5775 Ampère / meter.
In het laatste deel van de beoordeling merken we op dat, ongeacht de formulering van de wet van volledige stromen, de essentie ongewijzigd blijft. In zijn eigen woorden kan dit als volgt worden weergegeven: het drukt de relatie uit tussen de stromen die dit circuit binnendringen en de magnetische velden die in de stof worden gecreëerd.
Ten slotte raden we aan om een nuttige video over het onderwerp van het artikel te bekijken:
Gerelateerde materialen: