Kirchhoff's eerste en tweede wet - een betaalbare uitleg
De eerste wet van Kirchhoff
De definitie van de eerste wet is: “De algebraïsche som van stromen die door een knooppunt stromen is nul. ' Je kunt een iets andere vorm zeggen: 'Hoeveel stromen stroomden in het knooppunt, hetzelfde aantal stroomde naar buiten, wat de constante van stroom aangeeft ”.
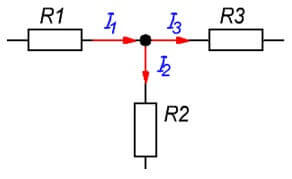
Een knooppunt van een ketting is een verbindingspunt van drie of meer takken. De stromen worden in dit geval verdeeld in verhouding tot de weerstand van elke tak.
ik1= Ik2+ Ik3
Deze vorm van opname is geldig voor DC-circuits. Als u de eerste Kirchhoff-wet gebruikt voor een wisselstroomcircuit, worden onmiddellijke spanningswaarden gebruikt, aangegeven met de letter İ en geschreven in complexe vorm, en de berekeningsmethode blijft hetzelfde:
De complexe vorm houdt rekening met zowel de actieve als reactieve componenten.
Tweede wet van Kirchhoff
Als de eerste de verdeling van stromen in de takken beschrijft, dan is de tweede wet van Kirchhoff: “De som van de spanningsdalingen in het circuit is gelijk aan de som van alle EMV's. ”In eenvoudige woorden luidt de formulering als volgt: “EMF toegepast op een sectie van een circuit zal worden verdeeld over de elementen van dit circuit in verhouding tot de weerstanden, d.w.z. volgens de wet van Ohm. "
Terwijl het voor wisselstroom als volgt klinkt: "De som van de amplituden van de complexe EMF is gelijk aan de som van de complexe spanningsdalingen op de elementen ".
Z is de impedantie of complexe weerstand, het omvat zowel het resistieve deel als het reactieve (inductie en capaciteit), dat afhangt van de frequentie van de wisselstroom (in gelijkstroom is er alleen actieve weerstand). Hieronder staan de formules van de complexe weerstand van de condensator en inductie:
Hier is een afbeelding die het bovenstaande illustreert:
Dan:
Berekeningsmethoden voor de eerste en tweede wetten van Kirchhoff
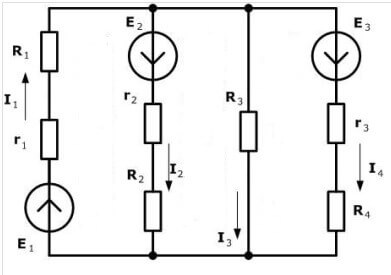
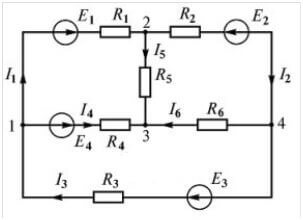
Laten we theoretisch materiaal in de praktijk brengen. Om tekens correct in de vergelijkingen te plaatsen, moet u de richting van het circuit kiezen. Bekijk het diagram:
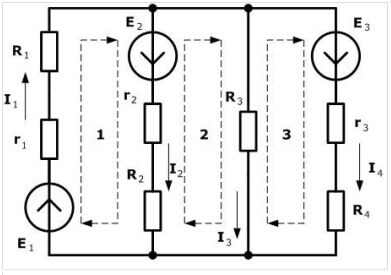
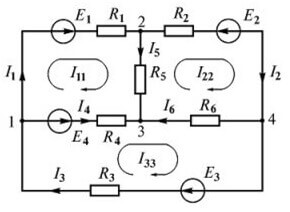
We raden aan om een richting met de klok mee te kiezen en deze in de afbeelding te markeren:
De gestippelde stippellijn geeft aan hoe het pad moet worden gevolgd bij het maken van vergelijkingen.
De volgende stap is het opstellen van vergelijkingen volgens de wetten van Kirchhoff. Eerst gebruiken we de tweede.We plaatsen de tekens op deze manier: een minteken wordt voor de elektromotorische kracht geplaatst als het tegen de klok in wordt gericht (de richting die we in de vorige stap hebben gekozen), en voor een emf met de klok mee plaatsen we een minteken. We stellen voor elk circuit samen, rekening houdend met de borden.
Voor de eerste kijken we naar de richting van de EMF, deze valt samen met de streep-stippellijn, set E1 plus E2:
Voor de tweede:
Voor de derde:
De tekens voor IR (spanning) zijn afhankelijk van de richting van de lusstromen. Hier is de tekenregel hetzelfde als in het vorige geval.
IR wordt met een positief teken geschreven als de stroom in de richting van de bypassrichting van het circuit stroomt. En met een "-" teken, als de stroom tegen de richting van het circuit in stroomt.
De richting van circuitverplaatsing is een voorwaardelijke grootheid. Het is alleen nodig voor het rangschikken van tekens in vergelijkingen, het wordt willekeurig gekozen en heeft geen invloed op de juistheid van berekeningen. In sommige gevallen kan een slecht gekozen bypass-richting de berekening bemoeilijken, maar dit is niet kritisch.
Overweeg een ander circuit:
Er zijn maar liefst vier bronnen van EMF, maar de berekeningsprocedure is hetzelfde, eerst kiezen we de richting voor het maken van de vergelijkingen.
Nu moet je vergelijkingen maken volgens de eerste wet van Kirchhoff. Voor het eerste knooppunt (figuur 1 aan de linkerkant van het diagram):
Ik3 stroomt in, en ik1, Ik4 het volgt, vandaar de tekenen. Voor de tweede:
Voor de derde:
Vraag: "Er zijn vier knooppunten en er zijn maar drie vergelijkingen, waarom? 'Het feit is dat het aantal vergelijkingen van de eerste Kirchhoff-regel gelijk is aan:
Nvergelijkingen= nknopen-1
D.w.z. er zijn slechts 1 vergelijkingen minder dan knooppunten, omdat dit is genoeg om de stromen in alle takken te beschrijven, ik adviseer nogmaals om naar het circuit te gaan en te controleren of alle stromen in de vergelijkingen zijn geschreven.
Nu gaan we over tot de constructie van vergelijkingen volgens de tweede regel. Voor het primaire circuit:
Voor het tweede circuit:
Voor het derde circuit:
Als we de waarden van echte spanningen en weerstanden vervangen, dan blijkt dat de eerste en tweede wet eerlijk zijn en worden vervuld. Dit zijn eenvoudige voorbeelden; in de praktijk moeten veel omvangrijkere problemen worden opgelost.
Conclusie. Het belangrijkste bij het berekenen met behulp van de eerste en tweede Kirchhoff-wetten is het naleven van de regel voor het maken van vergelijkingen, houd rekening met de richting van de stroom en de bypass van het circuit voor de juiste plaatsing van tekens voor elk element van het circuit.
Kirchhoffs wetten voor het magnetische circuit
Berekeningen van magnetische circuits zijn ook belangrijk in de elektrotechniek, beide wetten hebben hier hun toepassing gevonden. De essentie blijft hetzelfde, maar het type en de grootte veranderen, laten we dit probleem in meer detail bekijken. Eerst moet je met concepten omgaan.
Magnetomotorische kracht (MDS) wordt bepaald door het product van het aantal windingen van de spoel, door de stroom er doorheen:
F = w * ik
Magnetische spanning is het product van magnetische veldsterkte en stroom door een sectie, gemeten in ampère:
Um= H * ik
Of magnetische flux door magnetische weerstand:
Um= F * Rm
L is de gemiddelde lengte van de plot, μr en μ0 - relatieve en absolute magnetische permeabiliteit.
Als we een analogie tekenen, schrijven we de eerste Kirchhoff-wet voor een magnetisch circuit:
Dat wil zeggen, de som van alle magnetische fluxen door het knooppunt is nul. Is het je opgevallen dat het bijna hetzelfde klinkt als voor een elektrisch circuit?
Dan klinkt de tweede wet van Kirchhoff als: 'De som van de MDS in het magnetische circuit is gelijk aan de som UM (magnetische spanning).
Magnetische flux is gelijk aan:
Voor een wisselend magnetisch veld:
Het hangt alleen af van de spanning over de wikkeling en niet van de parameters van het magnetische circuit.
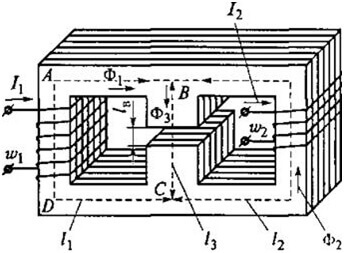
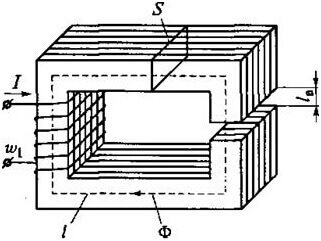
Beschouw bijvoorbeeld deze contour:
Dan krijgen we voor ABCD de volgende formule:
Voor circuits met een luchtspleet zijn de volgende relaties waar:
Magnetische weerstand:
En de weerstand van de luchtspleet (rechts op de kern):
Waar S het kerngebied is.
Om het materiaal volledig te begrijpen en enkele nuances van het gebruik van de regels visueel te bekijken, raden we u aan om vertrouwd te raken met de lezingen die op de video worden gegeven:
De ontdekkingen van Gustav Kirchhoff hebben een belangrijke bijdrage geleverd aan de ontwikkeling van de wetenschap, met name elektrotechniek.Met hun hulp is het vrij eenvoudig om elk elektrisch of magnetisch circuit, stromen erin en spanningen te berekenen. We hopen dat Kirchhoff's regels voor elektrische en magnetische circuits nu duidelijker voor je worden.
Vergelijkbare materialen:

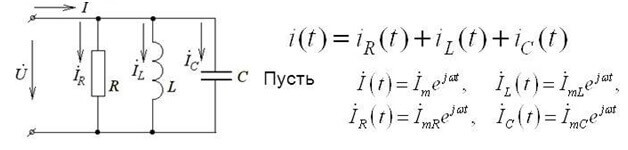
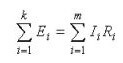
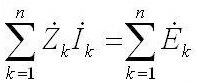
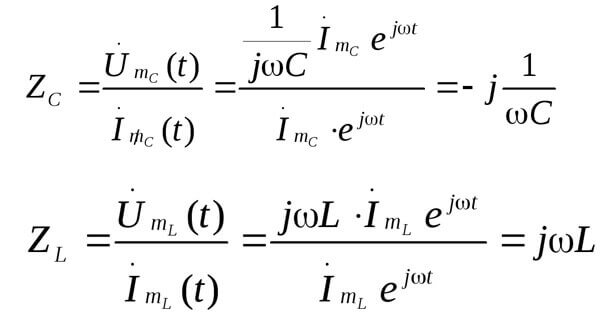

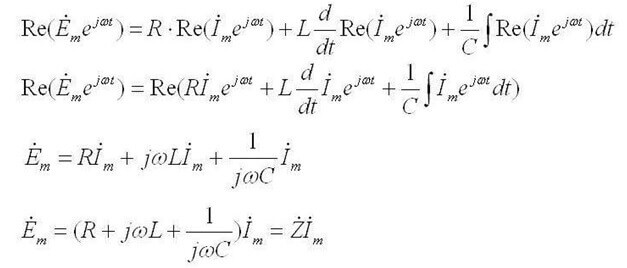
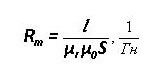
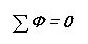
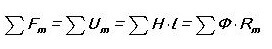
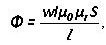
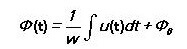
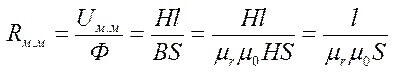
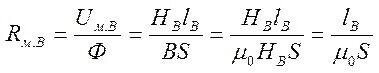


Als we u samenstellen volgens de eerste wet van Kirchhoff, dat wil zeggen, een goede uitleg van de eerste ur. Waarom is er geen verklaring voor de tweede en derde, terwijl alles daar veel onduidelijker is? I2 stroomt daar duidelijk binnen, maar om de een of andere reden heeft hij een positief teken
in de derde vergelijking, dus over het algemeen stromen alle drie ik in. Waarom zijn ze positief?
Houd er rekening mee dat aan het begin van het artikel de vergelijking wordt beschouwd in de vorm I1 = I2 + I3, als u alles naar de linkerkant van de vergelijking overbrengt, I1-I2-I3 = 0. Hetzelfde werd daar gedaan.
Voor het tweede knooppunt:
I1 = I5 + I2
alles in één richting verplaatsen komt naar buiten:
I1-I5-I2 = 0
In vergelijking met de richting van de circuitbypass, wordt het duidelijk dat het beter is om de tekens te veranderen, dat wil zeggen vermenigvuldigen met min 1.
Zal uitkomen
-I1 + I5 + I2 = 0
wat equivalent is
I2 + I5-I1 = 0