Kiršhofa pirmais un otrais likums - pieņemams skaidrojums
Pirmais Kiršhofa likums
Pirmā likuma definīcija ir šāda:"Algebriska straumju summa, kas plūst caur mezglu, ir nulle." Jūs varat pateikt nedaudz atšķirīgu formu: "Cik strāvas ieplūda mezglā, izplūda tas pats skaitlis, kas norāda uz strāvas noturību ”.
Ķēdes mezgls ir savienojuma punkts no trim vai vairāk zariem. Strāvas šajā gadījumā tiek sadalītas proporcionāli katras filiāles pretestībai.
Es1= Es2+ Es3
Šis ierakstīšanas veids ir derīgs līdzstrāvas ķēdēm. Ja maiņstrāvas ķēdē izmantojat pirmo Kiršhofa likumu, tad tiek izmantotas momentānās sprieguma vērtības, tiek apzīmētas ar burtu İ un uzrakstītas sarežģītā formā, un aprēķina metode paliek tā pati:
Sarežģītajā formā tiek ņemti vērā gan aktīvie, gan reaktīvie komponenti.
Kirchhoff otrais likums
Ja pirmais apraksta straumju sadalījumu zaros, tad otrais Kiršhofa likums ir šāds: “Ķēdes sprieguma kritumu summa ir vienāda ar visu EML summu. ”Vienkāršiem vārdiem sakot, formulējums ir šāds: “EML, kas tiek piemērots kādas shēmas sekcijai, tiks sadalīts starp šīs shēmas elementiem proporcionāli pretestībai, t.i. saskaņā ar Ohmas likumiem. "
Tā kā maiņstrāvai tas izklausās šādi: “Kompleksa EML amplitūdu summa ir vienāda ar kompleksa sprieguma kritumu summu uz elementiem ".
Z ir pretestība vai kompleksa pretestība, tajā ietilpst gan pretestīgā daļa, gan reaktīvā daļa (induktivitāte un kapacitāte), kas ir atkarīga no maiņstrāvas frekvences (tiešajā strāvā ir tikai aktīvā pretestība). Zemāk ir kondensatora kompleksās pretestības un induktivitātes formulas:
Šeit ir attēls, kas ilustrē iepriekš minēto:
Tad:
Pirmā un otrā Kiršhofa likuma aprēķināšanas metodes
Pievērsīsimies teorētiskā materiāla ieviešanai praksē. Lai pareizi izvietotu zīmes vienādojumos, jums jāizvēlas ķēdes virziens. Apskatiet diagrammu:
Mēs iesakām izvēlēties virzienu pulksteņrādītāja virzienā un atzīmēt to attēlā:
Punktēta punktēta līnija norāda, kā sekot ceļam, veidojot vienādojumus.
Nākamais solis ir vienādojumu sastādīšana saskaņā ar Kirhhofa likumiem. Vispirms mēs izmantojam otro.Mēs novietojam zīmes šādā veidā: mīnus zīme tiek novietota elektromotora spēka priekšā, ja tā ir vērsta pretēji pulksteņrādītāja virzienam (virziens, kuru mēs izvēlējāmies iepriekšējā solī), tad pulksteņrādītāja kustības virzienā emf mēs ievietojam mīnusa zīmi. Mēs sastādām katru shēmu, ņemot vērā zīmes.
Pirmo mēs skatāmies uz EML virzienu, tas sakrīt ar domuzīmi ar punktētu līniju, kas ir E1 plus E2:
Par otro:
Par trešo:
IR (sprieguma) pazīmes ir atkarīgas no cilpas strāvas virziena. Šajā gadījumā zīmju noteikums ir tāds pats kā iepriekšējā gadījumā.
IR tiek uzrakstīts ar pozitīvu zīmi, ja strāva plūst ķēdes apvedceļa virzienā. Un ar zīmi “-”, ja strāva plūst pret ķēdes virzienu.
Ķēdes šķērsošanas virziens ir nosacīts lielums. Tas ir vajadzīgs tikai zīmju izvietojumam vienādojumos, tas ir izvēlēts patvaļīgi un neietekmē aprēķinu pareizību. Dažos gadījumos slikti izvēlēts apvedceļa virziens var sarežģīt aprēķinu, taču tas nav kritiski.
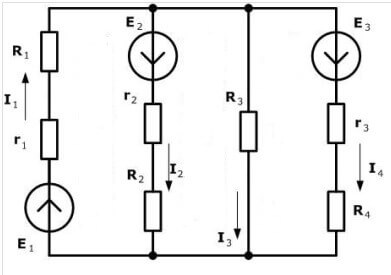
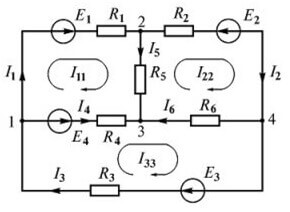
Apsveriet citu ķēdi:
Ir pat četri EML avoti, taču aprēķināšanas procedūra ir vienāda, vispirms mēs izvēlamies vienādojumu veidošanas virzienu.
Tagad jums ir jāizveido vienādojumi saskaņā ar Kirhhofa pirmo likumu. Pirmajam mezglam (1. attēls diagrammas kreisajā pusē):
Es3 ieplūst, un es1, Es4 no tā izriet, līdz ar to arī zīmes. Par otro:
Par trešo:
Jautājums: "Kāpēc ir četri mezgli, un ir tikai trīs vienādojumi, kāpēc? ”Fakts ir tāds, ka pirmā Kiršhofa noteikuma vienādojumu skaits ir vienāds ar:
Nvienādojumi= nmezgli-1
T. i. ir tikai par 1 mazāk vienādojumu nekā mezgliem, jo ar to pietiek, lai aprakstītu straumes visās atzarās, es iesaku vēlreiz aiziet līdz ķēdei un pārbaudīt, vai visas strāvas ir ierakstītas vienādojumos.
Tagad mēs pārejam pie vienādojumu konstruēšanas pēc otrā noteikuma. Primārajai shēmai:
Otrajai shēmai:
Trešajai shēmai:
Ja mēs aizstājam reālo spriegumu un pretestību vērtības, tad izrādās, ka pirmais un otrais likums ir taisnīgi un tiek izpildīti. Šie ir vienkārši piemēri, praksē ir jāatrisina daudz apjomīgākas problēmas.
Secinājums. Galvenais, veicot aprēķinus ar pirmā un otrā Kiršhofa likuma palīdzību, ir vienādojumu veidošanas noteikuma ievērošana, t.i. pareizam zīmju izvietojumam katram ķēdes elementam ņem vērā strāvas plūsmas virzienu un ķēdes apvedceļu.
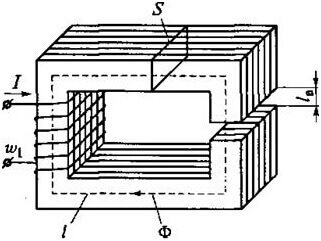
Kiršofa likumi par magnētisko ķēdi
Magnētisko ķēžu aprēķini ir svarīgi arī elektrotehnikā, abi likumi šeit ir atraduši savu pielietojumu. Būtība nemainās, bet mainās tips un lielums, apskatīsim šo jautājumu sīkāk. Vispirms jums jānodarbojas ar koncepcijām.
Magnetomotora spēku (MDS) nosaka ar spoles pagriezienu skaita reizinājumu ar caur to plūstošo strāvu:
F = w * i
Magnētiskais spriegums ir magnētiskā lauka stipruma un strāvas caur sekciju reizinājums, mērot ampēros:
Um= H * I
Vai magnētiskā plūsma caur magnētisko pretestību:
Um= F * Rm
L ir grafika vidējais garums, μr un μ0 - relatīvā un absolūtā magnētiskā caurlaidība.
Zīmējot analoģiju, mēs uzrakstām pirmo Kiršofa likumu magnētiskajai shēmai:
Tas ir, visu magnētisko plūsmu summa caur mezglu ir nulle. Vai esat pamanījis, ka tas izklausās gandrīz tāpat kā elektriskās ķēdes gadījumā?
Tad Kiršofa otrais likums izklausās šādi: “MDS summa magnētiskajā ķēdē ir vienāda ar summu UM (magnētiskais spriegums).
Magnētiskā plūsma ir vienāda ar:
Mainīgam magnētiskajam laukam:
Tas ir atkarīgs tikai no sprieguma tinumā, nevis no magnētiskās ķēdes parametriem.
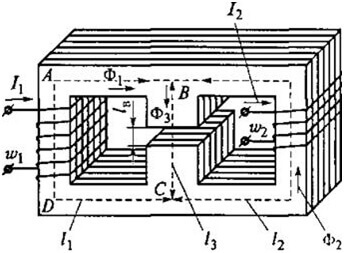
Kā piemēru apsveriet šo kontūru:
Tad ABCD mēs iegūstam šādu formulu:
Ķēdēm ar gaisa spraugu ir spēkā šādas attiecības:
Magnētiskā pretestība:
Un gaisa spraugas pretestība (labajā pusē uz serdes):
Kur S ir galvenā zona.
Lai pilnībā izprastu materiālu un vizuāli pārskatītu dažas noteikumu lietošanas nianses, iesakām iepazīties ar lekcijām, kas tiek piedāvātas video:
Gustava Kiršhofa atklājumi deva nozīmīgu ieguldījumu zinātnes, it īpaši elektrotehnikas, attīstībā.Ar viņu palīdzību ir diezgan vienkārši aprēķināt jebkuru elektrisko vai magnētisko ķēdi, tajā esošās strāvas un spriegumus. Mēs ceram, ka tagad Kiršhofa noteikumi par elektriskajām un magnētiskajām ķēdēm jums kļūs skaidrāki.
Līdzīgi materiāli:

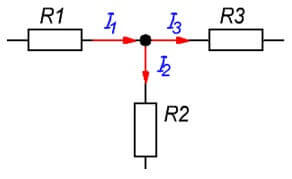
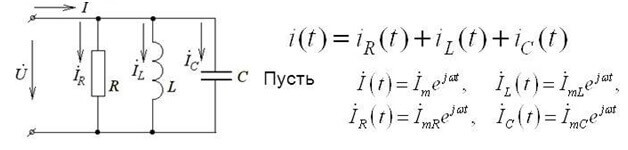
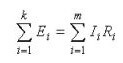
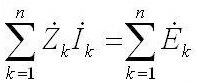
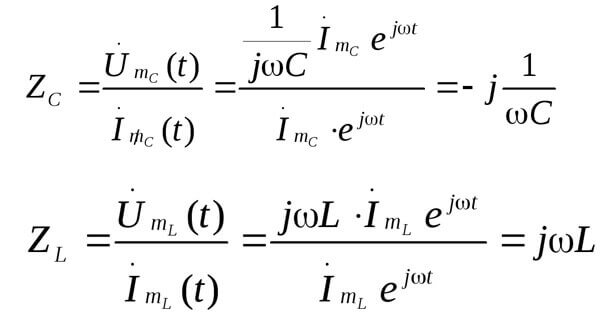

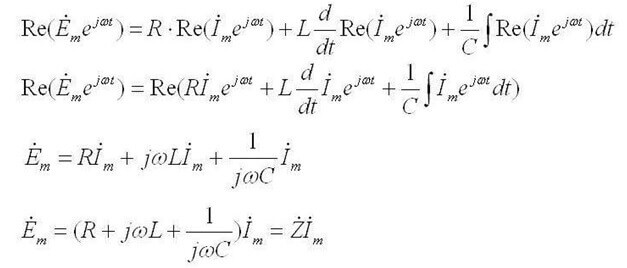
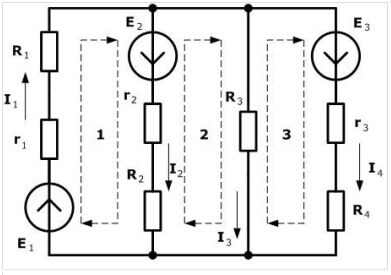
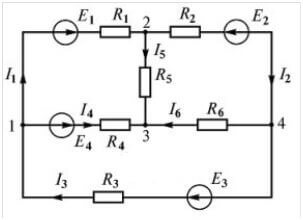
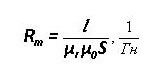
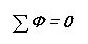
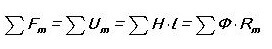
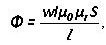
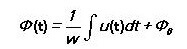
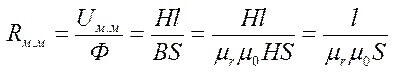
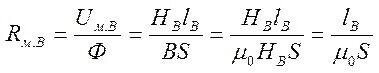


Kad mēs sastādām ur saskaņā ar Kirhhoff pirmo likumu, tas ir, labs pirmā ur skaidrojums. Kāpēc nav izskaidrojums otrajam un trešajam, kad tur viss ir daudz nemanāmāk? I2 nepārprotami ieplūst tur, bet kaut kādu iemeslu dēļ viņam ir pozitīva zīme
trešajā vienādojumā, tātad visi trīs es ieeju iekšā. Kāpēc viņi ir pozitīvi?
Lūdzu, ņemiet vērā, ka raksta sākumā vienādojums tiek uzskatīts formā I1 = I2 + I3, ja visu pārnesat vienādojuma kreisajā pusē, I1-I2-I3 = 0. Tas pats tika darīts tur.
Otrajam mezglam:
I1 = I5 + I2
pārvietojot visu vienā virzienā, iznāks:
I1-I5-I2 = 0
Salīdzinot ar ķēdes apvedceļa virzienu, kļūst skaidrs, ka labāk ir mainīt zīmes, tas ir, reizināt ar mīnus 1.
Iznāks
-I1 + I5 + I2 = 0
kas ir līdzvērtīgs
I2 + I5-I1 = 0