Kokonaisvirran laki yksinkertaisin sanoin
Tunnettu aihe, nimeltään Sähkötekniikka, sisältää ohjelmaansa sarjan peruslakeja, jotka määrittelevät fyysisen vuorovaikutuksen periaatteet magneettikentälle. Ne laajentavat vaikutuksensa sähkölaitteiden eri osiin, samoin kuin niiden rakenteisiin ja ympäristöön. Niissä tapahtuvien prosessien fysiikka koskee sellaisia peruskäsitteitä kuin sähkövirrat ja kentät. Kokonaisvirran laki vahvistaa suhteen sähkövarausten liikkumisen ja sen luoman magneettikentän (tarkemmin sen voimakkuuden) välillä. Moderni tiede väittää, että sen soveltaminen ulottuu melkein kaikkiin ympäristöihin.
Lain ydin
Magneettipiireihin sovellettava harkittu laki määrittää seuraavan kvantitatiivisen suhteen sen komponenttien välillä. Magneettikenttävektorin kierto suljetussa silmukassa on verrannollinen sitä tunkeutuvien virtojen summaan. Kokonaisvirran lain fyysisen merkityksen ymmärtämiseksi sinun on perehdyttävä hänen kuvaamiensa prosessien graafiseen esitykseen.
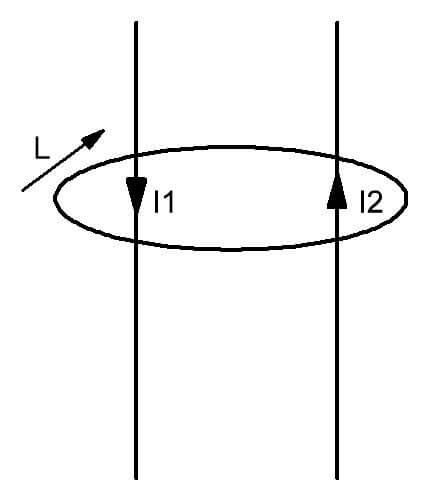
Kuviosta voidaan nähdä, että noin kahdella johtimella, joiden virtaukset I1 ja I2 virtaavat niiden läpi, muodostuu kenttä, jota rajoittaa piiri L. Se on esitetty henkisesti kuvitelluna suljettuna kuvana, jonka tason lävitsevät liikkuvien varausten johtimet. Yksinkertaisin sanoin tämä laki voidaan ilmaista seuraavasti. Useiden sähkövirtojen läsnä ollessa piirin L peittämän kuvitteellisen kuvitteellisen pinnan läpi muodostuu magneettikenttä, jolla on tietty jännitysjakauma.
Vektorin positiiviseen suuntaan magneettipiirin muodon lain mukaisesti valitaan myötäpäivään. Se on myös kuviteltavissa.
Tällainen virtausten luoma pyörrekentän määritelmä viittaa siihen, että jokaisen virran suunta voi olla mielivaltainen.
Viitteeksi! Esitetty kenttärakenne ja sitä kuvaava laite on erotettava sähköstaattisen vektorin “E” kiertämisestä, joka on aina yhtä suuri kuin nollan ohittaminen piiri. Tämän seurauksena tällainen kenttä viittaa potentiaalisiin rakenteisiin. Magneettikentän vektorin ”B” kierto ei ole koskaan nolla. Siksi sitä kutsutaan ”pyörreksi”.
Peruskäsitteet
Tarkasteltavana olevan lain mukaisesti magneettikenttien laskemiseksi käytetään seuraavaa yksinkertaistettua lähestymistapaa. Kokonaisvirta esitetään suljetun piirin L peittämän pinnan läpi virtaavien useiden komponenttien summana. Teoreettiset laskelmat voidaan esittää seuraavasti:
- Piirien ing I läpi virtaava kokonaisvirtavirta on vektorien I1 ja I2 summa.
- Määritä tässä esimerkissä kaava seuraavalla tavalla:
ΣI = I1 - I2 (miinus ennen toista termiä tarkoittaa, että virtojen suunnat ovat vastakkaiset). - Ne puolestaan määritetään sähkötekniikassa tunnetun lain (sääntö) mukaisesti näveri.
Radan magneettikenttä lasketaan erikoistekniikoilla saatujen laskelmien perusteella. Sen löytämiseksi on välttämätöntä integroida tämä parametri L: ään käyttämällä Maxwellin yhtälöä, joka on esitetty yhdessä muodossa.Sitä voidaan soveltaa differentiaalimuodossa, mutta se vaikeuttaa laskelmia jonkin verran.
Yksinkertaistettu integroitu lähestymistapa
Jos käytämme differentiaalista esitystä, kokonaisvirran lain ilmaistaminen yksinkertaistetussa muodossa on erittäin vaikeaa (tässä tapauksessa siihen on lisättävä lisäkomponentteja). Lisäämme tähän, että piirissä liikkuvien virtojen muodostama magneettinen pyörrekenttä määritetään tässä tapauksessa ottamalla huomioon esijännitevirta, joka riippuu sähköisen induktion muutosnopeudesta.
Siksi käytännössä, TOE: ssä, suositeltavampi on kaavojen esittäminen täysvirroille kaavioiden mikroskooppisesti pienten segmenttien summaamisen muodossa, jossa niihin on muodostettu pyörrekentät. Tämä lähestymistapa sisältää Maxwell-yhtälön soveltamisen kiinteässä muodossa. Kun se toteutetaan, ääriviivat jaetaan pieniin segmentteihin, joita pidetään ensimmäisessä lähentämisessä suoraviivaisina (lain mukaan oletetaan, että magneettikenttä on homogeeninen). Tämä arvo, jota merkitään Um tyhjössä toimivan magneettikentän yhden erillisen osan ΔL pituudelle, määritetään seuraavasti:
Um = HL * AL
Kokonaisjännitys koko muotoa L pitkin, esitetty lyhyesti kiinteässä muodossa, saadaan seuraavasta kaavasta:
UL = Σ HL * ΔL.
Tyhjiön kokonaisvirran laki
Lopullisessa muodossaan, joka on laadittu kaikkien integraatiosääntöjen mukaisesti, kokonaisvirran laki näyttää tältä. Vektorin "B" kierto kierto suljetussa silmukassa voidaan esittää magneettisen vakion tulona m virtausten määränä:
B: n integraali yli dL = Bl: n integraali yli dL = m Σ Sisään
missä n on niiden johtimien kokonaismäärä, joissa on monisuuntaisia virtauksia, jotka on peitetty mielivaltaisesti mielivaltaisen muodon piirillä L.
Jokainen virta otetaan huomioon tässä kaavassa niin monta kertaa, kuin se kattaa tämän piirin kokonaan.
Saatu laskelmien lopulliseen muotoon kokonaisvirran lain suhteen vaikuttaa suuresti väliaine, jossa indusoitu sähkömagneettinen voima (kenttä) toimii.
Ympäristövaikutukset
Ei tyhjiössä, vaan magneettisessa väliaineessa toimivien virtojen ja kenttien suhteen tarkastellut suhteet ovat hiukan erilaisessa muodossa. Tässä tapauksessa päävirtakomponenttien lisäksi otetaan käyttöön esimerkiksi magneetissa tai missä tahansa sen kaltaisessa materiaalissa syntyvien mikroskooppisten virtojen käsite.
Tarvittava suhde johdetaan kokonaisuudessaan lauseesta magneettisen induktion B vektorikiertoon. Yksinkertaisesti sanottuna se ilmaistaan seuraavassa muodossa. Vektorin B kokonaisarvo integroituna valitulle piirille on yhtä suuri kuin sen kattamien makrovirtojen summa kerrottuna magneettisen vakion kertoimella.
Seurauksena aineen "B" kaava määritetään lausekkeella:
B: n integraali yli dL = Bl: n integraali yli dL = m(minä+minä1)
missä: dL on piirin diskreetti elementti ohituksensa pitkin, Bl on komponentti tangentin suunnassa mielivaltaisessa pisteessä, bI ja I1 ovat johtamisvirta ja mikroskooppinen (molekyyli) virta.
Jos kenttä toimii mielivaltaisista materiaaleista koostuvassa ympäristössä, näille rakenteille ominaiset mikroskooppiset virrat on otettava huomioon.
Nämä laskelmat ovat totta myös solenoidiin tai muuhun väliaineeseen, jonka magneettinen läpäisevyys on luotu, muodostetulle kentälle.
Viitteeksi
GHS: n kattavimmassa ja kattavimmassa mittausjärjestelmässä magneettikentän voimakkuus on esitetty Oerstedsissä (E). Toisessa olemassa olevassa järjestelmässä (SI) se ilmaistaan ampeereina metriä kohti (A / metri). Nykyään oersted korvataan vähitellen käytännöllisemmällä yksiköllä - ampeeria metriä kohti.Muunnettaessa mittausten tai laskelmien tuloksia SI: stä GHS: ään, käytetään seuraavaa suhdetta:
1 E = 1000 / (4π) A / m ≈ 79,5775 ampeeri / m.
Katsauksen viimeisessä osassa huomaamme, että riippumatta siitä, mitä täyden virran lain sanamuotoa käytetään, sen olemus pysyy muuttumattomana. Hänen omien sanojensa mukaan tämä voidaan esittää seuraavasti: se ilmaisee tämän piirin tunkeutuvien virtojen ja aineeseen muodostettujen magneettikentien välisen suhteen.
Lopuksi suosittelemme katsomaan hyödyllistä videota artikkelin aiheesta:
Aiheeseen liittyvät materiaalit: