Kirchhoffin ensimmäinen ja toinen laki - edullinen selitys
Kirchhoffin ensimmäinen laki
Ensimmäisen lain määritelmä on seuraava:Solmun läpi virtaavien virtojen algebrallinen summa on nolla. ” Voit sanoa hieman erilaisen muodon: "Kuinka monta virtaa virtai solmuun, sama luku virtaa ulos, mikä osoittaa virran vakion ”.
Ketjun solmu on kolmen tai useamman haaran yhteyspiste. Tässä tapauksessa virrat jakautuvat suhteessa kunkin haaran vastukseen.
minä1= Minä2+ Minä3
Tämä tallennusmuoto on voimassa tasavirtapiireille. Jos käytät ensimmäistä Kirchhoff-lakia vaihtovirtapiirille, silloin käytetään hetkellisiä jännitearvoja, merkitään kirjaimella İ ja kirjoitetaan monimutkaisessa muodossa, ja laskentatapa pysyy samana:
Monimutkaisessa muodossa otetaan huomioon sekä aktiiviset että reaktiiviset komponentit.
Kirchhoffin toinen laki
Jos ensimmäinen kuvaa virtojen jakautumista oksilla, toinen Kirchhoffin laki on seuraava:Piirissä olevien jännitehäviöiden summa on yhtä suuri kuin kaikkien EMF: ien summa. "Yksinkertaisin sanoin sanamuoto on seuraava: ”Piirin osaan sovellettu EMF jakautuu tämän piirin elementtien kesken suhteessa resistanssiin, ts. Ohmin lain mukaan. "
Muuttuvan virran suhteen se kuulostaa tältä: "Kompleksin EMF: n amplitudien summa on yhtä suuri kuin elementtien jännitepudotusten summa ".
Z on impedanssi tai kompleksinen vastus, se sisältää sekä resistiivisen osan että reaktiivisen osan (induktanssi ja kapasitanssi), mikä riippuu vaihtovirran taajuudesta (tasavirralla on vain aktiivinen vastus). Alla on kaavat kondensaattorin monimutkaisesta resistanssista ja induktanssista:
Tässä on kuva, joka kuvaa yllä olevaa:
sitten:
Kirchhoffin ensimmäisen ja toisen lain laskentamenetelmät
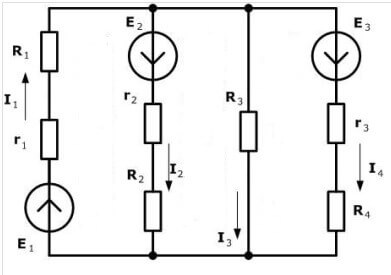
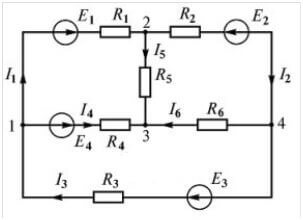
Siirrytään teoreettisen materiaalin toteuttamiseen käytännössä. Jotta merkit voidaan sijoittaa oikein yhtälöihin, sinun on valittava piirin suunta. Katso kaavio:
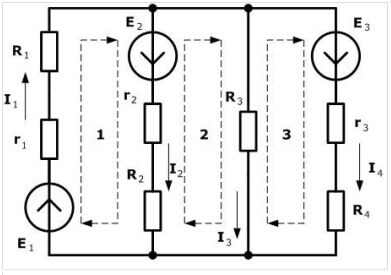
Ehdotamme valita myötäpäivään ja merkitä se kuvassa:
Katkoviivoitettu viiva osoittaa, kuinka seurata polkua yhtälöitä tehtäessä.
Seuraava vaihe on yhdistää yhtälöt Kirchhoffin lakien mukaisesti. Ensin käytämme toista.Laitamme merkit näin: miinusmerkki sijoitetaan sähkövoiman eteen, jos se on suunnattu vastapäivään (edellisessä vaiheessa valitsemamme suunta), sitten myötäpäivään emf laitamme miinusmerkin. Me säveltämme jokaiselle piirille ottaen huomioon merkit.
Ensimmäisenä tarkastellaan EMF: n suuntaa, se on samansuuntainen katkoviivalla, asetettu E1 plus E2:
Toiseksi:
Kolmannesta:
IR (jännitteen) merkit riippuvat silmukkavirtojen suunnasta. Tässä merkkisääntö on sama kuin edellisessä tapauksessa.
IR kirjoitetaan positiivisella merkillä, jos virta virtaa piirin ohitussuunnan suuntaan. Ja "-" -merkillä, jos virta virtaa piirin suuntaa vasten.
Piirin kulkusuunta on ehdollinen määrä. Sitä tarvitaan vain merkkien järjestelyyn yhtälöissä, se on valittu mielivaltaisesti eikä vaikuta laskelmien oikeellisuuteen. Joissain tapauksissa huonosti valittu ohitussuunta voi vaikeuttaa laskentaa, mutta tämä ei ole kriittistä.
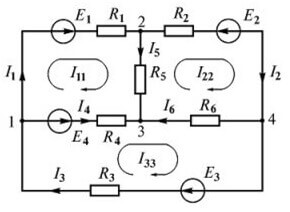
Harkitse toista piiriä:
EMF-lähteitä on peräti neljä, mutta laskentatapa on sama, ensin valitaan yhtälöiden muodostamissuunta.
Nyt sinun on tehtävä yhtälöt Kirchhoffin ensimmäisen lain mukaan. Ensimmäinen solmu (kuva 1 kaavion vasemmalla puolella):
minä3 virtaa sisään, ja minä1, Minä4 se seuraa, siis merkkejä. Toiseksi:
Kolmannesta:
Kysymys: "Miksi? Neljä solmua on ja yhtälöitä on vain kolme, miksi? "Tosiasia on, että ensimmäisen Kirchhoff-säännön yhtälöiden lukumäärä on yhtä suuri kuin:
Nyhtälöt= nsolmua-1
eli yhtälöitä on vain 1 vähemmän kuin solmuja, koska tämä riittää kuvaamaan kaikkien haarojen virtauksia, kehotan jälleen kerran menemään piirille ja tarkistamaan, onko kaikki virrat kirjoitettu yhtälöihin.
Nyt siirrymme yhtälöiden muodostamiseen toisen säännön avulla. Ensiöpiirille:
Toinen piiri:
Kolmas piiri:
Jos korvaamme todellisten jännitteiden ja vastusten arvot, niin käy ilmi, että ensimmäinen ja toinen laki ovat oikeudenmukaiset ja täyttyvät. Nämä ovat yksinkertaisia esimerkkejä, käytännössä on ratkaistava paljon laajemmat ongelmat.
johtopäätös. Tärkein asia laskettaessa ensimmäisen ja toisen Kirchhoff-lain avulla on yhtälöiden muodostamissäännön noudattaminen, ts. ota huomioon virran virtaussuunta ja piirin ohitus merkkien oikeassa järjestelyssä jokaiselle piirin elementille.
Kirchhoffin lait magneettipiiristä
Magneettipiirien laskelmat ovat tärkeitä myös sähkötekniikassa, molemmat lait ovat löytäneet sovelluksen täällä. Pohjimmiltaan pysyy samana, mutta tyyppi ja koko muuttuvat, katsokaamme tätä asiaa yksityiskohtaisemmin. Ensin on käsiteltävä käsitteitä.
Magnetomoottorivoima (MDS) määritetään kelan kierrosten lukumäärän ja sen läpi kulkevan virran kertoimella:
F = w * i
Magneettinen jännite on osan magneettikentän voimakkuuden ja virran tulo, mitattuna ampeereina:
Um= H * I
Tai magneettinen virta magneettisen vastuksen kautta:
Um= F * Rm
L on kuvaajan keskimääräinen pituus, μR ja μ0 - suhteellinen ja absoluuttinen magneettinen läpäisevyys.
Piirrämme analogian kirjoittamalla ensimmäisen Kirchhoffin lain magneettipiirille:
Eli kaikkien solmun läpi kulkevien magneettivuojen summa on nolla. Oletko huomannut, että kuulostaa melkein samalta kuin sähköpiiriltä?
Sitten Kirchhoffin toinen laki kuulostaa seuraavalta: “MDS: n summa magneettipiirissä on yhtä suuri kuin summa UM (magneettinen rasitus).
Magneettinen flux on yhtä suuri kuin:
Vaihtelevaa magneettikenttää varten:
Se riippuu vain käämin ylittävästä jännitteestä, ei magneettisen piirin parametreista.
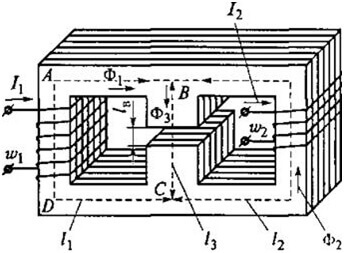
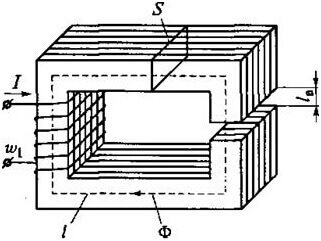
Mieti esimerkiksi tätä muotoa:
Sitten saamme ABCD: lle seuraavan kaavan:
Ilmarakoilla varustetuissa piireissä seuraavat suhteet ovat totta:
Magneettinen vastus:
Ja ilmaraon vastus (ytimen oikealla puolella):
Missä S on ydinalue.
Materiaalin ymmärtämiseksi kokonaan ja joidenkin sääntöjen käytön vivahteiden tarkastelemiseksi visuaalisesti suosittelemme, että tutustut videossa oleviin luentoihin:
Gustav Kirchhoffin löytöillä oli merkittävä vaikutus tieteen, etenkin sähkötekniikan, kehitykseen.Heidän avullaan on melko helppoa laskea mikä tahansa sähkö- tai magneettinen piiri, siinä olevat virrat ja jännitteet. Toivomme, että nyt Kirchhoffin säännöt sähkö- ja magneettipiireistä tulevat sinulle selkeämmiksi.
Samanlaisia materiaaleja:

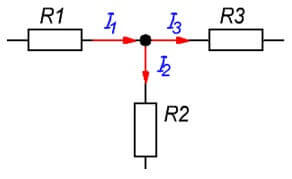
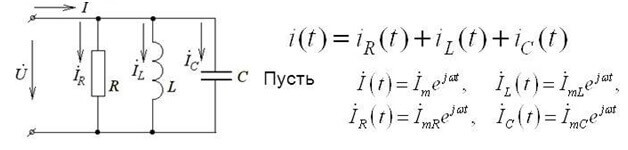
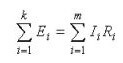
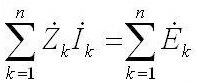
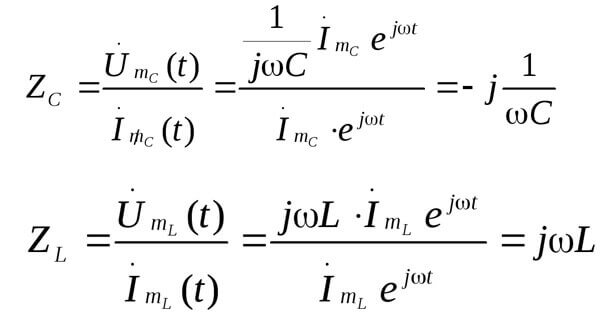

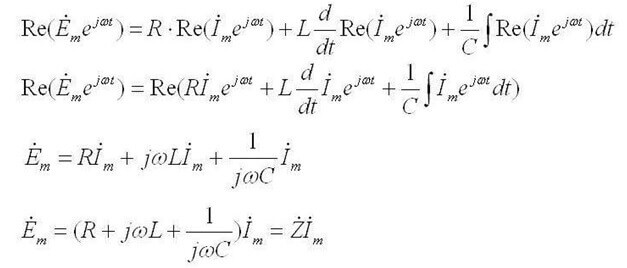
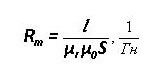
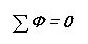
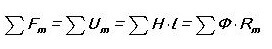
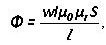
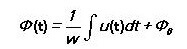
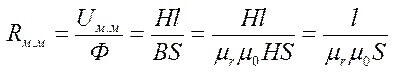
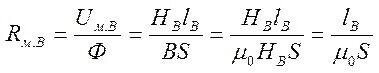


Kun me sävelemme ur Kirchhoffin ensimmäisen lain mukaan, se on hyvä selitys ensimmäiselle urille. Miksi toiselle ja kolmannelle ei ole selitystä, kun kaikki on siellä paljon selkeämpää? I2 virtaa selvästi sinne, mutta jostain syystä hänellä on positiivinen merkki
kolmannessa yhtälössä, joten yleensä kaikki kolme virtaan sisään. Miksi ne ovat positiivisia?
Huomaa, että artikkelin alussa yhtälöä pidetään muodossa I1 = I2 + I3, jos siirrät kaiken yhtälön vasemmalle puolelle, I1-I2-I3 = 0. Sama asia tehtiin siellä.
Toiselle solmulle:
I1 = I5 + I2
kaiken siirtäminen yhteen suuntaan tulee ulos:
I1-I5-I2 = 0
Verrattuna piirin ohituksen suuntaan käy selväksi, että on parempi muuttaa merkkejä, ts. Kertomalla miinus 1.
Tulee ulos
-I1 + I5 + I2 = 0
mikä vastaa
I2 + I5-I1 = 0