Kuinka löytää virtapiiri piiristä

Jos virta ja jännite tunnetaan

Oletetaan, että joudut löytämään virtapiiri piiristä, kun tiedät vain jännitteen ja virrankulutuksen. Määritä sitten se ilman vastustusta kaavalla:

P = UI

Yksinkertaisen jälkeen saamme kaavan laskelmiin

I = P / U

On huomattava, että tämä lauseke pätee tasavirtapiireihin. Mutta esimerkiksi sähkömoottorin laskelmissa otetaan huomioon sen täysi teho tai kosini Phi. Sitten kolmivaihemoottorille se voidaan laskea seuraavasti:

Löydämme P ottaen huomioon tehokkuuden, yleensä se on välillä 0,75–0,88:

P1 = P2 / η

Tässä P2 on akselin aktiivinen nettovoima, η - hyötysuhde,molemmat parametrit osoittavat yleensä tyyppikilven.

Löydämme kokonaistehon ottaen huomioon cosФ (se on myös ilmoitettu tyyppikilvessä):

S = P1 / cosφ

Määritämme nykyisen kulutuksen kaavalla:

Inom = S / (1,73 · U)

Tässä 1,73 on 3: n juuri (jota käytetään kolmivaiheisen piirin laskemiseen), U on jännite, riippuu moottorin käynnistyksestä (kolmio tai tähti) ja verkon jännitteiden lukumäärästä (220, 380, 660 jne.). Vaikka maassamme, 380 V löytyy useimmiten.

Jos jännite tai teho ja vastus tunnetaan

Mutta on ongelmia, kun tiedät piirin jännitteen ja kuorman suuruuden, kun haluat löytää virran ilman virtaa, käytä Ohmin lakilaskemme sen avulla virran lujuuden resistanssin ja jännitteen kautta.

I = U / R

Mutta joskus tapahtuu, että joudut määrittämään virranvoimakkuuden ilman jännitettä, ts. Kun tiedät vain piirin tehon ja sen vastuksen. Tässä tapauksessa:

P = UI

Lisäksi Ohmin saman lain mukaan:

U = IR

mitä:

P = i²* R

Joten suoritamme laskennan kaavan mukaan:

minä²= P / R

Tai ota lausekkeen oikealla puolella oleva lauseke juuri alla:

I = (P / R)^1/2

Jos EMF, sisäinen vastus ja kuorma tunnetaan

Opiskelijoiden saaliin liittyvissä ongelmissa on tapauksia, joissa sinulle annetaan EMF: n suuruus ja virtalähteen sisäinen vastus. Tässä tapauksessa voit määrittää virran voimakkuuden piirissä Ohmin lain mukaan täydelliselle piirille:

I = E / (R + r)

Tässä E on EMF, r on virtalähteen sisäinen vastus ja R on kuorma.

Joule-Lenzin laki

Toinen tehtävä, johon jopa enemmän tai vähemmän kokenut opiskelija voi päästä stuporiin, on virran voimakkuuden määrittäminen, jos aika, vastus ja johtimen vapauttaman lämmön määrä tiedetään.Tätä me muistamme Joule-Lenzin lakia.

Hänen kaavansa näyttää tältä:

Q = I²rt

Suorita sitten laskenta seuraavasti:

minä²= QRt

Tai lisää yhtälön oikea puoli juuren alle:

I = (Q / Rt)^1/2

Joitakin esimerkkejä

Päätelmänä ehdotamme, että saadut tiedot korjataan useisiin esimerkkeihin tehtävistä, joista sinun on löydettävä nykyinen vahvuus.

1 tehtävä: Laske I kahden vastuksen piirissä sarja- ja rinnakkaisliitäntää varten. R-vastukset 1 ja 2 ohmia, 12 voltin virtalähde.

Edellytyksestä on selvää, että jokaiselle yhdisteiden muunnelmalle on annettava kaksi vastausta. Sitten, kun haluat löytää virran sarjayhteydessä, lisää ensin piirin resistanssi saadaksesi kokonaisarvo.

R₁+ R₂= 1 + 2 = 3 ohmia

Sitten voit laskea virran voimakkuuden Ohmin lain mukaan:

I = U / R = 12/3 = 4 ampeeria

Kahden elementin rinnankytkennällä Rtotal voidaan laskea seuraavasti:

Rtotal = (R1 * R2) / (R1 + R2) = 1 * 2/3 = 2/3 = 0,67

Sitten lisälaskelmat voidaan suorittaa seuraavasti:

I = 12 * 0,67 = 18A

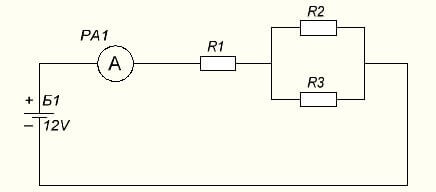
2 tehtävä: laske virta elementtien sekayhteydelle. Virtalähteen lähtö on 24 V, ja vastukset ovat: R1 = 1 ohmi, R2 = 3 ohmia, R3 = 3 ohmia.

Ensinnäkin, sinun on löydettävä R yhteinen rinnakkain kytketyissä R2: ssa ja R3: ssa saman kaavan mukaisesti, jota käytimme yllä.

Rpriv = (R2 * R3) / (R2 + R3) = (3 * 3) | (3 + 3) = 9/6 = 3/2 = 1,5 ohmia

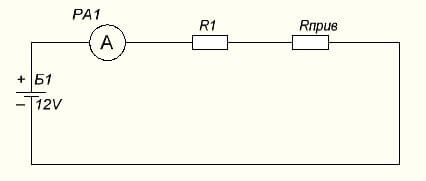
Nyt piiri on muodossa:

Seuraavaksi löydämme virran saman Ohmin lain mukaan:

I = U / (R1 + Rpriv) = 24 / (1 + 1,5) = 24 / 2,5 = 9,6 ampeeria

Nyt tiedät kuinka löytää virran voimakkuus, tietäen teho, vastus ja jännite. Toivomme, että toimitetut kaavat ja laskentaesimerkit auttoivat sinua oppimaan materiaalia!

Et todellakaan tiedä:

• Kuinka laskea kaapelin poikkileikkaus
• Kuinka muuntaa ampeereita kilowatteiksi
• Kuinka löytää johdin seinästä