Loven om total strøm med enkle ord
Det emne, der er kendt for mange, med titlen ”Elektroteknik”, indeholder i sit program en række grundlæggende love, der definerer principperne for fysisk interaktion for et magnetfelt. De udvider deres virkning til forskellige elementer i elektriske apparater såvel som deres strukturer og miljøer. Fysikken i de processer, der forekommer i dem, vedrører sådanne grundlæggende begreber som strøm af elektricitet og felt. Loven om total strøm skaber et forhold mellem bevægelsen af elektriske ladninger og det magnetiske felt, der er skabt af det (mere præcist dens intensitet). Moderne videnskab hævder, at dens anvendelse strækker sig til næsten alle miljøer.
Essensen af loven
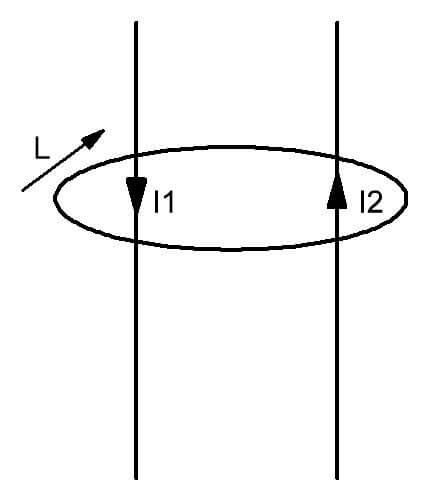
Den betragtede lov, der finder anvendelse i magnetiske kredsløb, bestemmer følgende kvantitative forhold mellem dets bestanddele. Cirkulationen af magnetfeltvektoren i en lukket sløjfe er proportional med summen af strømme, der trænger ind i den. For at forstå den fysiske betydning af loven om total strøm, skal du gøre dig bekendt med den grafiske repræsentation af de processer, der er beskrevet af ham.
Det ses af figuren, at omkring to ledere med strømme I1 og I2, der strømmer gennem dem, dannes et felt, begrænset af kredsløbet L. Det indføres som en mentalt forestillet lukket figur, hvis plan er gennemboret af ledere med bevægelige ladninger. Med enkle ord kan denne lov udtrykkes som følger. I nærværelse af adskillige strømme af elektricitet gennem den tænkte imaginære overflade, der er dækket af kredsløbet L, dannes der et magnetfelt med en given spændingsfordeling inden i det.
For den positive retning af vektoren i overensstemmelse med loven for konturen af det magnetiske kredsløb vælges med uret. Det kan også tænkes.
En sådan definition af hvirvelfeltet oprettet af strømme antyder, at retningen af hver af strømmerne kan være vilkårlig.
Til reference! Den indførte feltstruktur og apparatet, der beskriver det, skal adskilles fra cirkulationen af den elektrostatiske vektor "E", som altid er lig med nul uden omløb af kredsløbet. Som et resultat af dette henviser et sådant felt til potentielle strukturer. Cirkulationen af vektoren "B" i magnetfeltet er aldrig nul. Derfor kaldes det en "virvel".
Basale koncepter
I overensstemmelse med den omtvistede lov anvendes følgende forenklede fremgangsmåde til beregning af magnetiske felter. Den samlede strøm er repræsenteret som summen af flere komponenter, der strømmer gennem en overflade dækket af et lukket kredsløb L. Teoretiske beregninger kan repræsenteres som følger:
- Den samlede elektriske strøm, der strømmer gennem kredsløbene Σ I, er vektorsummen af I1 og I2.
- Brug formlen til at bestemme det i dette eksempel:
ΣI = I1 - I2 (minus før anden term betyder, at de nuværende retninger er modsat). - De er til gengæld bestemt efter den lov, der er kendt inden for elektroteknik (regel) gimlet.
Magnetfeltet langs konturen beregnes på grundlag af beregningerne opnået ved hjælp af specielle teknikker. For at finde det er det nødvendigt at integrere denne parameter over L ved hjælp af Maxwell-ligningen præsenteret i en af formerne.Det kan anvendes i differentiel form, men dette vil komplicere beregningerne noget.
Forenklet integreret tilgang
Hvis vi bruger den differentielle repræsentation, vil det at udtrykke loven for den samlede strøm i en forenklet form være meget vanskeligt (i dette tilfælde skal der indføres yderligere komponenter i det). Vi tilføjer til dette, at det magnetiske virvelfelt, der oprettes af strømme, der bevæger sig inden i kredsløbet, bestemmes i dette tilfælde under hensyntagen til forspændingsstrømmen, der afhænger af hastigheden for ændring af elektrisk induktion.
Derfor i praksis, i TOE, er præsentationen af formler for fulde strømme i form af en sammenlægning af mikroskopisk små segmenter af et kredsløb med virvelfelter oprettet i dem mere populær. Denne tilgang involverer anvendelse af Maxwell-ligningen i integreret form. Når den implementeres, er konturen opdelt i små segmenter, der anses for at være ligetil i den første tilnærmelse (ifølge loven antages det, at magnetfeltet er homogent). Denne værdi, betegnet som Um for et diskret afsnit af længden ΔL af det magnetiske felt, der virker i vakuum, er defineret som følger:
Um = HL * ΔL
Den totale spænding langs den fulde kontur L, der præsenteres kort i integreret form, findes ved følgende formel:
UL = Σ HL * ΔL.
Loven om den samlede strøm for vakuum
I sin endelige form, der er udarbejdet i henhold til alle integrationsregler, ser lovgivningen om den samlede strøm sådan ud. Cirkulation af vektoren "B" i en lukket sløjfe kan repræsenteres som produktet af den magnetiske konstant m i mængden af strømme:
Integralet af B over dL = integralet af Bl over dL = m Σ I
hvor n er det samlede antal ledere med multidirektionsstrømme, der er dækket af et mentalt forestillet kredsløb L af vilkårlig form.
Hver strøm tages i betragtning i denne formel så mange gange, som den er helt dækket af dette kredsløb.
Den endelige form for de opnåede beregninger for loven om total strøm påvirkes i høj grad af det medium, i hvilket den inducerede elektromagnetiske kraft (felt) virker.
Miljømæssig påvirkning
De betragtede forhold for loven om strømninger og felter, der ikke fungerer i et vakuum, men i et magnetisk medium, har en lidt anden form. I dette tilfælde introduceres ud over hovedstrømkomponenterne begrebet mikroskopiske strømme, der for eksempel opstår i en magnet eller i ethvert materiale der ligner det.
Den nødvendige relation er fuldt ud afledt af teoremet om vektorcirkulationen af magnetisk induktion B. Enkelt udtrykt udtrykkes det i følgende form. Den samlede værdi af vektoren B, når den er integreret over det valgte kredsløb, er lig med summen af de makrostrømme, der er dækket af den ganget med koefficienten for magnetkonstanten.
Som et resultat bestemmes formlen for "B" i et stof ved udtrykket:
Integralet af B over dL = integralet af Bl over dL = m(jeg+jeg1)
hvor: dL er det diskrete element i kredsløbet langs dets bypass, Bl er komponenten i retning af tangenten på et vilkårligt punkt, bI og I1 er ledningsstrømmen og den mikroskopiske (molekylære) strøm.
Hvis feltet fungerer i et miljø, der består af vilkårlige materialer, bør de mikroskopiske strømme, der er karakteristisk for disse strukturer, tages i betragtning.
Disse beregninger gælder også for det felt, der er oprettet i solenoiden eller i et hvilket som helst andet medium med endelig magnetisk permeabilitet.
Til reference
I det mest komplette og omfattende system til måling af GHS er magnetfeltstyrken repræsenteret i Oersteds (E). I et andet eksisterende system (SI) udtrykkes det i ampere pr. Meter (A / meter). I dag erstattes osted gradvist af en mere praktisk enhed i drift - en ampere pr. Meter.Når man oversætter resultaterne af målinger eller beregninger fra SI til GHS, anvendes følgende forhold:
1 E = 1000 / (4π) A / m ≈ 79,5775 Ampere / meter.
I den sidste del af gennemgangen bemærker vi, at uanset hvilken formulering af loven om fulde strømme bruges, forbliver dens essens uændret. Med sine egne ord kan dette repræsenteres som følger: det udtrykker forholdet mellem strømme, der trænger ind i et givet kredsløb, og de magnetiske felter, der er skabt i stoffet.
Endelig anbefaler vi, at du ser en nyttig video om artiklets emne:
Relaterede materialer: