Kirchhoffs første og anden lov - Overkommelig forklaring
Kirchhoffs første lov
Definitionen af den første lov er: “Den algebraiske sum af strømme, der strømmer gennem en knude, er nul. ” Du kan sige en lidt anden form: "Hvor mange strømme flydede ind i noden, det samme antal flydede ud, hvilket indikerer strømmenes konstant ”.
En knudepunkt i en kæde er et forbindelsespunkt for tre eller flere grene. Strømmene i dette tilfælde er fordelt i forhold til modstanden for hver gren.
jeg1= Jeg2+ Jeg3
Denne form for optagelse er gyldig for DC-kredsløb. Hvis du bruger den første Kirchhoff-lov til et vekselstrømskredsløb, anvendes øjeblikkelige spændingsværdier, betegnes med bogstavet İ og skrives i kompleks form, og beregningsmetoden forbliver den samme:
Den komplekse form tager højde for både de aktive og reaktive komponenter.
Anden lov af Kirchhoff
Hvis den første beskriver fordelingen af strømme i grenene, er den anden Kirchhoff-lov:Summen af spændingsfaldene i kredsløbet er lig med summen af alle EMF'er. ”I enkle ord lyder ordlyden som følger: ”EMF anvendt på et afsnit af et kredsløb vil blive fordelt mellem elementerne i dette kredsløb i forhold til modstanderne, dvs. ifølge Ohms lov. "
Med hensyn til vekselstrøm lyder det sådan: “Summen af amplituderne af det komplekse EMF er lig med summen af de komplekse spændingsfald på elementerne ".
Z er den totale modstand eller den komplekse modstand, den inkluderer både den resistive del og den reaktive (induktans og kapacitans), der afhænger af frekvensen af vekselstrømmen (i jævnstrøm er der kun aktiv modstand). Nedenfor er formlerne for den komplekse modstand af kondensatoren og induktansen:
Her er et billede, der illustrerer ovenstående:
Derefter:
Beregningsmetoder til Kirchhoffs første og anden lovgivning
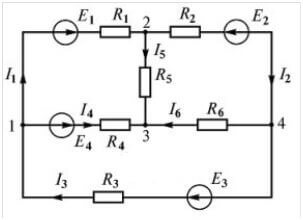
Lad os komme til at omsætte teoretisk materiale i praksis. For at placere tegn korrekt i ligningerne skal du vælge kredsløbets retning. Se på diagrammet:
Vi foreslår at vælge en med uret og markere den på figuren:
Den stiplede linje angiver, hvordan man følger stien, når man foretager ligninger.
Det næste trin er at komponere ligninger i henhold til Kirchhoffs love. Først bruger vi det andet.Vi sætter skiltene sådan: et minustegn placeres foran elektromotorisk kraft, hvis det er rettet mod uret (den retning, vi valgte i det forrige trin), derefter sætter vi et minustegn for højre emf. Vi komponerer for hvert kredsløb under hensyntagen til skiltene.
For det første ser vi på EMF's retning, det falder sammen med den stiplede linje, sæt E1 plus E2:
For det andet:
For det tredje:
Skiltene til IR (spænding) afhænger af retningen på loopstrømmene. Her er skiltreglen den samme som i det foregående tilfælde.
IR skrives med et positivt tegn, hvis strømmen flyder i retning af kredsløbets bypass-retning. Og med et "-" tegn, hvis strømmen flyder mod kredsløbets retning.
Retningen for kredsløbskørsel er en betinget mængde. Det er kun nødvendigt for arrangementet af tegn i ligninger, det vælges vilkårligt og påvirker ikke beregningernes rigtighed. I nogle tilfælde kan en dårligt valgt bypass-retning komplicere beregningen, men dette er ikke kritisk.
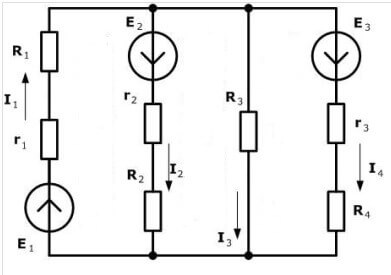
Overvej et andet kredsløb:
Der er så mange som fire kilder til EMF, men beregningsproceduren er den samme. Først vælger vi retningen for at fremstille ligningerne.
Nu skal du foretage ligninger i henhold til Kirchhoffs første lov. For den første knude (figur 1 til venstre for diagrammet):
jeg3 strømmer ind, og jeg1, Jeg4 det følger, følgelig tegnene. For det andet:
For det tredje:
Spørgsmål: "Der er fire noder, og der er kun tre ligninger, hvorfor? ”Faktum er, at antallet af ligninger for den første Kirchhoff-regel er lig med:
Nligninger= nknob-1
dvs. der er kun 1 mindre ligninger end knudepunkter, fordi dette er nok til at beskrive strømme i alle grene, jeg råder endnu en gang til at gå op til kredsløbet og kontrollere, om alle strømme er skrevet i ligningerne.
Nu går vi videre til konstruktion af ligninger efter den anden regel. For det primære kredsløb:
For det andet kredsløb:
For det tredje kredsløb:
Hvis vi erstatter værdierne for reelle spændinger og modstande, viser det sig, at den første og anden lov er fair og er opfyldt. Dette er enkle eksempler; i praksis skal meget mere omfangsrige problemer løses.
konklusion. Det vigtigste ved beregning ved hjælp af den første og anden Kirchhoff-lovgivning er overholdelsen af reglen for fremstilling af ligninger, dvs. tage højde for strømningsretningen og kredsløbskontakten for det korrekte arrangement af skilte for hvert element i kredsløbet.
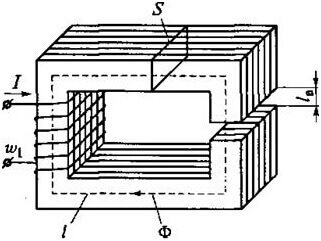
Kirchhoffs love for magnetisk kredsløb
Beregninger af magnetiske kredsløb er også vigtige inden for elektroteknik, begge love har fundet deres anvendelse her. Essensen forbliver den samme, men typen og størrelsen ændres, lad os se på dette spørgsmål mere detaljeret. Først skal du håndtere koncepter.
Magnetomotiv kraft (MDS) bestemmes af produktet af antallet af spoler, og strømmen igennem det:
F = w * i
Magnetspænding er produktet af magnetfeltstyrke og strøm gennem et snit, målt i Amperes:
Um= H * I
Eller magnetisk flux gennem magnetisk modstand:
Um= F * Rm
L er plotets gennemsnitlige længde μr og μ0 - relativ og absolut magnetisk permeabilitet.
Når vi tegner en analogi, skriver vi den første Kirchhoff-lov for et magnetisk kredsløb:
Det vil sige, summen af alle magnetiske fluxer gennem noden er nul. Har du bemærket, at det lyder næsten det samme som for et elektrisk kredsløb?
Så lyder Kirchhoffs anden lov som ”Summen af MDS i magnetkredsløbet er lig med summen UM (magnetisk spænding).
Magnetisk flux er lig med:
For et vekslende magnetfelt:
Det afhænger kun af spændingen over viklingen og ikke af parametrene for magnetkredsløbet.
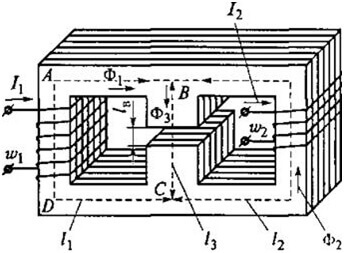
Som et eksempel skal du overveje denne kontur:
Så for ABCD får vi følgende formel:
For kredsløb med et luftspalte er de følgende forhold sande:
Magnetisk modstand:
Og modstanden fra luftspalten (til højre på kernen):
Hvor S er kerneområdet.
For fuldt ud at forstå materialet og visuelt gennemgå nogle af nuancerne ved at bruge reglerne, anbefaler vi, at du sætter dig ind i forelæsningerne, der findes på videoen:
Opdagelserne af Gustav Kirchhoff gav et betydeligt bidrag til udviklingen af videnskab, især elektroteknik.Med deres hjælp er det ganske enkelt at beregne ethvert elektrisk eller magnetisk kredsløb, strømme i det og spændinger. Vi håber, at Kirchhoffs regler for elektriske og magnetiske kredsløb nu bliver mere tydelige for dig.
Lignende materialer:

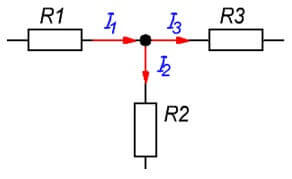
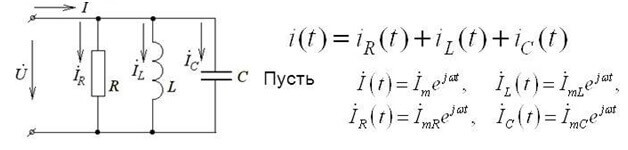
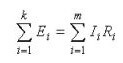
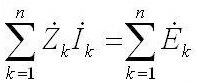
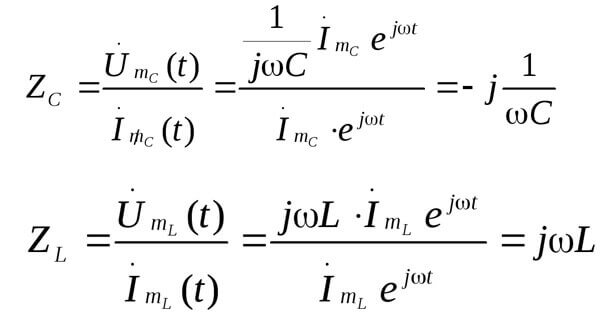

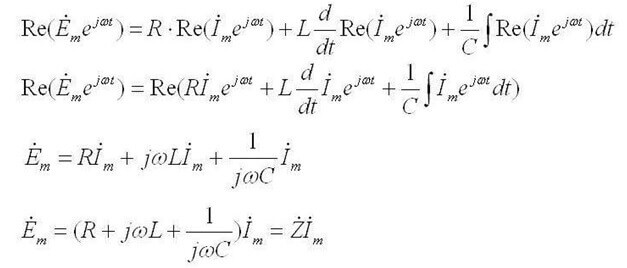
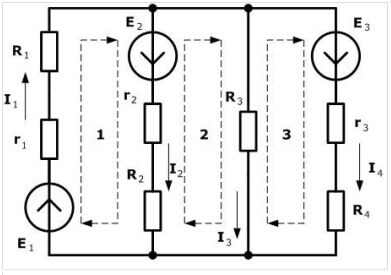
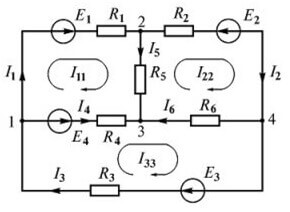
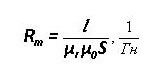
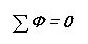
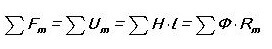
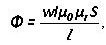
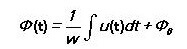
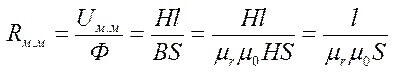
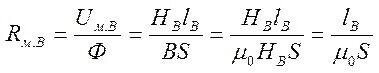


Når vi komponerer ur i henhold til Kirchhoffs første lov, det vil sige en god forklaring af den første ur. Hvorfor er der ingen forklaring på det andet og det tredje, når alt er meget mere uvidende der? I2 flyder klart derinde, men af en eller anden grund har han et positivt tegn
i den tredje ligning, så generelt løber jeg alle tre ind. Hvorfor er de positive?
Bemærk, at ligningen i begyndelsen betragtes som formen I1 = I2 + I3, hvis du overfører alt til venstre side af ligningen, I1-I2-I3 = 0. Den samme ting blev gjort der.
For den anden knude:
I1 = I5 + I2
bevægelse af alt i en retning vil komme ud:
I1-I5-I2 = 0
Sammenlignet med retningen på kredsløbskontakten bliver det klart, at det er bedre at ændre skiltene, dvs. multiplicere med minus 1.
Vil komme ud
-I1 + I5 + I2 = 0
hvilket er ækvivalent
I2 + I5-I1 = 0