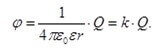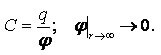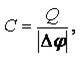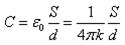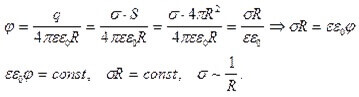Hvordan ladninger fordeles i en leder, når strømmen strømmer
Ladere og deres bevægelse
En leder er et stof, hvor bærere begynder at bevæge sig under påvirkning af det mindste eksterne elektriske felt. Når der ikke er noget eksternt felt, annullerer felterne med positive ioner og negative elektroner hinanden. Vi undersøgte et relateret problem mere detaljeret og sammenlignede ledere, dielektrik og halvledere i en artikel offentliggjort tidligere.
Overvej et metalgenstande, der er i et elektrisk felt. Ladningsbærerne begynder at bevæge sig under påvirkning af et eksternt felt på grund af det faktum, at Coulomb-styrkerne begynder at handle på ladningsbærerne. Derudover ligger retningen for disse kræfter på positive og negative bærere i en anden retning. Bevægelsen stopper, hvis summen af intensiteten af de eksterne og indre felter bliver nul, det vil sige:
Eres = E intern + E ekstern = 0
I dette tilfælde er feltstyrken lig med:
E = dF / dt
Hvis spændingen er nul, er potentialet inde i kroppen lig med et konstant tal. Dette vil blive klart, hvis vi udtrykker potentialet fra denne formel og integrerer, det vil sige:
Positive ioner og elektroner fra hele kropsvolumen haster til dens overflade for at kompensere for spændingen elektrisk felt. Derefter inden i lederen bliver det elektriske felt lig med nul, da det er afbalanceret af ladningsbærere fra dets overflade.
Interessant! En overflade, hvor det samme potentiale er til stede på alle punkter, kaldes ekvipotential.
Hvis vi overvejer dette spørgsmål mere detaljeret, bevæger positive ioner sig, når en leder indføres i et elektrisk felt, mod dens kraftlinjer og negative elektroner i samme retning. Dette sker, indtil de er fordelt, og feltet i lederen bliver lig med nul. Sådanne afgifter kaldes induceret eller overskydende.
Vigtig! Når ladningerne formidles til det ledende materiale, fordeles de således, at der opnås en ligevægtstilstand. De samme ladninger frastøder og tendens i overensstemmelse med retningen på det elektriske felts kraftlinjer.
Det følger, at arbejdet med at flytte ladningsfirmaer er nul, hvilket er lig med potentialeforskellen. Derefter er potentialet i forskellige sektioner af lederen lig med et konstant tal og ændres ikke.Det er vigtigt at vide, at i et dielektrikum, for at rive en ladningsbærer af, for eksempel en elektron fra et atom, skal store kræfter anvendes. Derfor observeres de beskrevne fænomener i generel forstand på ledende organer.
Elektrisk kapacitet af en ensartet leder
Overvej først begrebet en enslig leder. Dette er en leder, der er fjernt fra andre ladede ledere og organer. Derudover afhænger potentialet af det af dets ladning.
Den elektriske kapacitet af en ensartet leder er en leders evne til at holde en distribueret ladning. Først og fremmest afhænger det af lederens form.
Hvis to sådanne legemer er adskilt af et dielektrikum, for eksempel luft, glimmer, papir, keramik osv. - få en kondensator. Dets kapacitet afhænger af afstanden mellem pladerne og deres område samt af den potentielle forskel mellem dem.
Formlerne beskriver kapacitansens afhængighed af potentialeforskellen og de geometriske dimensioner af en flad kondensator. Lær mere om hvad er elektrisk kapacitet, kan du fra vores separate artikel.
Ladefordeling og kropsform
Så afhængigheden af ladningsbærere afhænger af lederens form. Overvej dette med eksemplet med formler for en sfære.
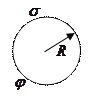
Antag, at vi har en bestemt metallisk ladet kugle, med radius R, ladningstæthed på overfladen G og potentiale F. Derefter:
Fra den sidst afledte formel kan vi forstå, at densiteten er omtrent omvendt proportional med sfærens radius.
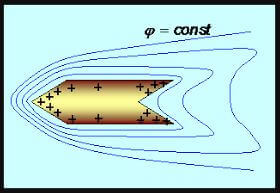
Det vil sige, at jo mere konveks og skarp genstand er, jo større er tætheden af bærere på dette sted. På konkave overflader er densiteten minimal. Dette kan ses i videoen:
Praktisk ansøgning
Hvis du tager højde for ovenstående, er det værd at bemærke, at strømmen strømmer gennem kablet og fordeles, som om rørets ydre diameter. Dette skyldes egenskaberne ved fordelingen af elektroner i et ledende legeme.
Det er underligt, at når strøm flyder i systemer med en højfrekvent strøm, observeres en hudeffekt. Dette er fordelingen af afgifter på overfladen af lederne. Men i dette tilfælde observeres et endnu tyndere "ledende" lag.
Hvad betyder det? Dette antyder, at for strømmen af strøm af samme størrelse med en netværksfrekvens på 50 Hz og en frekvens på 50 kHz i et højfrekvenskredsløb, kræves et større tværsnit af den ledende kerne. I praksis observeres dette ved at skifte strømforsyning. Det er netop sådanne strømme, der strømmer i deres transformere. For at øge tværsnitsarealet skal du enten vælge en tyk ledning eller vikle viklingerne med flere årer på én gang.
Afhængigheden af densitetsfordelingen på overfladeformen beskrevet i det foregående afsnit anvendes i praksis i lynbeskyttelsessystemer. Det er kendt, at en af typerne af lynbeskyttelse, for eksempel en lynstang, er installeret for at beskytte mod lynskader. På dens overflade ophobes ladede partikler, på grund af hvilken udledningen forekommer nøjagtigt i det, hvilket igen bekræfter, hvad der blev sagt om deres distribution.
Endelig anbefaler vi at se en video, hvor det med enkle ord forklares og grafisk vises, hvordan ladningerne er fordelt i lederen:
Dette er alt, hvad vi ønskede at fortælle dig om, hvordan ladningsfordelingen i lederen sker, når strømmen strømmer. Vi håber, at de givne oplysninger var forståelige og nyttige for dig!
Relaterede materialer: