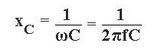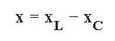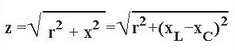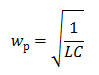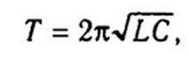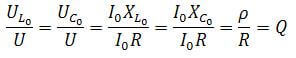Hvad er resonansen for strømme og spændinger

Induktansreaktans og kapacitans

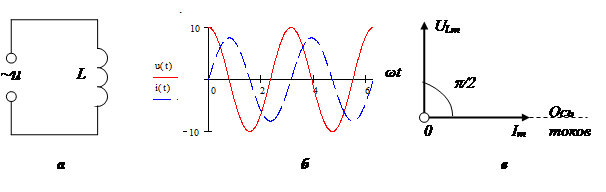
Induktans er kroppens evne til at akkumulere energi i et magnetfelt. Det er kendetegnet ved en forsinkelse af strøm fra spænding i fase. Typiske induktive elementer er choker, spoler, transformere, elektriske motorer.

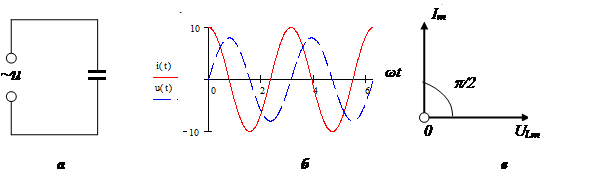
Kapacitet henviser til elementer, der lagrer energi gennem et elektrisk felt. Kapacitive elementer er kendetegnet ved en faseforsinkelse af spænding fra strøm. Kapacitive elementer: kondensatorer, varicaps.

Deres grundlæggende egenskaber er angivet, nuancerne i denne artikel tages ikke med i betragtning.

Ud over de anførte elementer har andre også en vis induktans og kapacitet, for eksempel i elektriske kabler fordelt langs dens længde.

Kapacitans og induktans i et vekselstrømskredsløb

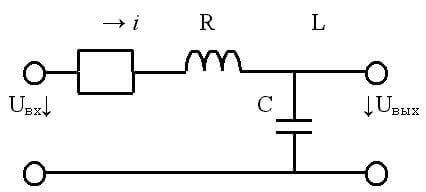
Hvis kapacitansen i jævnstrømskredse i generel forstand er en ødelagt del af kredsløbet, og induktansen er en leder, er vekselvise kondensatorer og spoler en reaktiv analog af en modstand.

Induktorens reaktion bestemmes af formlen:

Vector diagram:

Kondensatorreaktion:

Her er w vinkelfrekvensen, f er frekvensen i sinusformet strømkreds, L er induktansen, C er kapacitansen.

Vector diagram:

Det er værd at bemærke, at formlen bruges til beregning af reaktive elementer forbundet i serie:

Bemærk, at den kapacitive komponent tages med et minustegn. Hvis den aktive komponent (modstand) også er til stede i kredsløbet, tilføj derefter i henhold til formlen for den Pythagoreiske teorem (baseret på vektordiagrammet):

Hvad afhænger reaktansen af? Reaktive egenskaber afhænger af kapacitansen eller induktansen såvel som frekvensen af ​​vekselstrømmen.

Hvis du ser på formlen for den reaktive komponent, kan du se, at ved bestemte værdier for den kapacitive eller induktive komponent, deres forskel vil være nul, så er kun modstanden tilbage i kredsløbet. Men dette er ikke alle funktionerne i en sådan situation.

Spændingsresonans

Hvis en kondensator og en induktor er serieforbundet med en generator, vil der, forudsat at deres reaktans er ens, forekomme en spændingsresonans. I dette tilfælde skal den aktive del Z være så lille som muligt.

Det er værd at bemærke, at induktans og kapacitans kun har reaktive egenskaber kun i idealiserede eksempler. I rigtige kredsløb og elementer er ledere altid aktiv modstand, selvom det er ekstremt lille.

Ved resonans forekommer en energiudveksling mellem induktoren og kondensatoren. I ideelle eksempler akkumuleres energi under den indledende forbindelse af en energikilde (generator) i kondensatoren (eller induktoren), og efter at den er slukket, forekommer uspændede svingninger på grund af denne udveksling.

Spændinger på induktanser og kapacitanser er omtrent de samme Ohms lov:

U = I / X

Hvor X er henholdsvis Xc-kapacitiv eller XL-induktans.

Et kredsløb bestående af induktans og kapacitans kaldes et oscillerende kredsløb. Dets hyppighed beregnes ved formlen:

Oscillationsperioden bestemmes af Thompson-formlen:

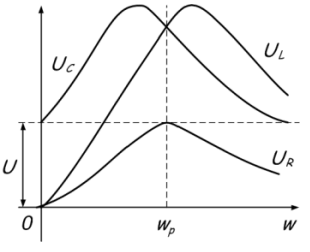
Da reaktansen afhænger af frekvensen, øges induktansmodstanden med stigende frekvens og falder ved kapacitansen. Når modstanderne er ens, reduceres den samlede modstand kraftigt, hvilket afspejles i grafen:

Kredsløbets vigtigste egenskaber er kvalitetsfaktoren (Q) og frekvensen. Hvis vi betragter kredsløbet som en fire-terminal, reduceres dens transmissionskoefficient efter enkle beregninger til kvalitetsfaktoren:

K = q

Og spændingen ved kredsløbets terminaler stiger i forhold til kredsløbets overførselskoefficient (kvalitetsfaktor).

UK = Uin * Q

Med spændingsresonans, jo højere kvalitetsfaktor, jo større vil spændingen på kredsløbselementerne overstige spændingen på den tilsluttede generator. Spændingen kan stige titusinde eller hundreder af gange. Dette vises i grafen:

Effekttab i kredsløbet skyldes kun tilstedeværelsen af ​​aktiv modstand. Energi fra strømkilden tages kun for at opretholde svingninger.

Kraftfaktoren vil være lig med:

cosФ = 1

Denne formel viser, at der opstår tab på grund af aktiv effekt:

S = P / Cosph

Resonansstrømme

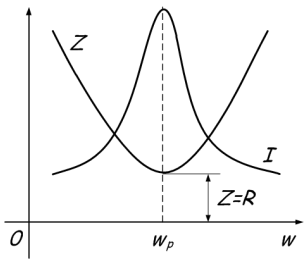
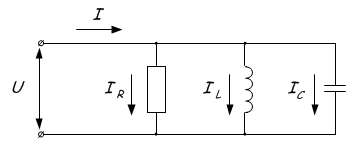
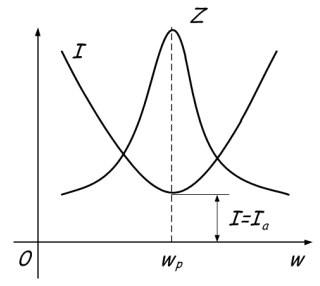
Aktuel resonans observeres i kredsløb, hvor induktansen og kapacitansen er parallelt forbundet.

Fænomenet består i strømmen af ​​store strømme mellem kondensatoren og spolen ved nulstrøm i den uforgrenede del af kredsløbet. Dette skyldes, at når resonansfrekvensen nås, øges den totale modstand Z. Eller simpelt set lyder det sådan - ved resonanspunktet nås den maksimale totale værdi af modstanden Z, hvorefter den ene af modstanderne øges, og den anden falder, afhængigt af om frekvensen øges eller formindskes. Dette vises grafisk:

Generelt ligner alt det tidligere fænomen, betingelserne for fremkomst af nuværende resonans er som følger:

1. Effektfrekvensen svarer til resonanten ved kredsløbet.
2. Konduktiviteterne i induktansen og kapacitansen for vekselstrøm er BL = Bc, B = 1 / X.

Praktisk anvendelse

Overvej fordelene og skadene ved resonansstrømme og spændinger. Den største fordel ved fænomenet resonans bragt i radiosenderudstyr. Med enkle ord har modtagerkredsløbet en spole og en kondensator forbundet til antennen. Ved at ændre induktansen (for eksempel at bevæge kernen) eller værdien af ​​kapacitansen (for eksempel en luftvariabel kondensator) justerer du resonansfrekvensen. Som et resultat stiger spændingen på spolen, og modtageren fanger en bestemt radiobølge.

Disse fænomener kan være skadelige i elektroteknik, for eksempel på kabellinjer. Et kabel er en induktans og kapacitans fordelt på længden, hvis der tilføres en spænding til en lang linje i tomgangstilstand (når belastningen ikke er forbundet til enden af ​​kablet modsat strømkilden). Derfor er der fare for, at der vil opstå en sammenbrud af isolering, for at undgå dette, er en belastningsforkobling forbundet.En lignende situation kan også føre til svigt i elektroniske komponenter, måleinstrumenter og andet elektrisk udstyr - dette er farlige konsekvenser af dette fænomen.

konklusion

Resonansen for spændinger og strømme er et interessant fænomen at være opmærksom på. Det observeres kun i induktive-kapacitive kredsløb. I kredsløb med store aktive modstande kan det ikke forekomme. For at opsummere, kort besvare de vigtigste spørgsmål om dette emne:

1. Hvor og i hvilke kæder observeres resonansfænomenet?

I induktive kapacitive kredsløb.

2. Hvad er betingelserne for forekomst af resonans af strømme og spændinger?

Det forekommer under betingelse af ens reaktans. Kredsløbet skal have en minimal aktiv modstand, og frekvensen af ​​strømforsyningen falder sammen med kredsløbets resonansfrekvens.

3. Hvordan finder jeg resonansfrekvensen?

I begge tilfælde med formlen:w = (1 / LC) ^ (1/2)

4. Hvordan fjerner man fænomenet?

Ved at øge modstanden i kredsløbet eller ændre frekvensen.

Nu ved du, hvad resonansen for strømme og spændinger er, hvad er betingelserne for dens forekomst og praktiske anvendelser. For at konsolidere materialet anbefaler vi at se en nyttig video om emnet:

Relaterede materialer:

• Årsagerne til tab af elektricitet over lange afstande
• AC-frekvensmåling
• Sådan beregnes trådmodstand