Primera i segona lleis de Kirchhoff: una explicació assequible
La primera llei de Kirchhoff
La definició de la primera llei és:"La suma algebraica de corrents que circulen per un node és zero." Podeu dir una forma una mica diferent: "Quants corrents van fluir al node, va sortir el mateix nombre, el que indica la constància del corrent ".
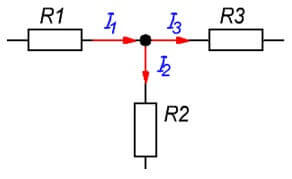
Un node d'una cadena és un punt de connexió de tres o més branques. Els corrents en aquest cas es distribueixen proporcionalment a la resistència de cada branca.
Jo1= Jo2+ Jo3
Aquesta forma d’enregistrament és vàlida per a circuits de corrent continu. Si utilitzeu la primera llei Kirchhoff per a un circuit de corrent altern, s'utilitzen valors de tensió instantània, que es denoten per la lletra İ i s'escriuen de forma complexa i el mètode de càlcul continua sent el mateix:
La forma complexa té en compte tant els components actius com els reactius.
Segona llei de Kirchhoff
Si el primer descriu la distribució de corrents en les branques, la segona llei Kirchhoff és:La suma de les caigudes de tensió al circuit és igual a la suma de tots els EMF. "En paraules simples, la redacció diu el següent: "EMF aplicat a una secció d'un circuit es distribuirà entre els elements d'aquest circuit en proporció a les resistències, segons la llei d'Ohm ".
Mentre que per corrent altern sona així: "La suma de les amplituds del complex EMF és igual a la suma de les caigudes de tensió complexes sobre els elements ".
La Z és la impedància o la resistència complexa, que inclou tant la part resistiva com la part reactiva (inductància i capacitança), que depèn de la freqüència del corrent altern (en corrent directe només hi ha resistència activa). A continuació es mostren les fórmules de la resistència complexa del condensador i la inductància:
Aquí teniu una imatge que il·lustra l’anterior:
Després:
Mètodes de càlcul de la primera i la segona llei de Kirchhoff
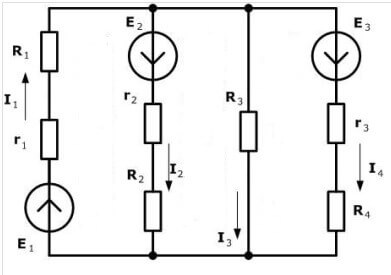
Comencem a posar en pràctica el material teòric. Per col·locar correctament els signes en les equacions, heu de triar la direcció del circuit. Mireu el diagrama:
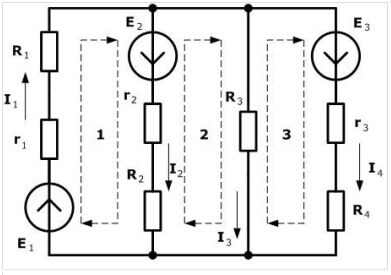
Us aconsellem triar una direcció en sentit horari i marcar-la a la figura:
La línia de guions puntejada indica com seguir el camí en fer equacions.
El següent pas és compondre equacions segons les lleis de Kirchhoff. El primer fem servir el segon.Posem els signes així: es posa un signe menys davant de la força electromotriu si es dirigeix en sentit antihorari (la direcció que vam triar al pas anterior), i després per emf un rellotge posem un signe menys. Redactem per a cada circuit tenint en compte els signes.
Per a la primera, mirem la direcció de l’EMF, coincideix amb la línia de guions puntejada, el conjunt E1 més E2:
Per a la segona:
Per a la tercera:
Els signes d’IR (tensió) depenen de la direcció dels corrents del bucle. Aquí la regla del signe és la mateixa que en el cas anterior.
L'IR s'escriu amb un signe positiu si el corrent flueix en el sentit de la direcció del circuit. I amb un signe "-", si la corrent flueix en contra de la direcció del circuit.
La direcció del recorregut del circuit és una quantitat condicionada. Només es necessita per a la disposició de signes en equacions, es tria arbitràriament i no afecta la correcció dels càlculs. En alguns casos, una direcció de desviació mal escollida pot complicar el càlcul, però això no és crític.
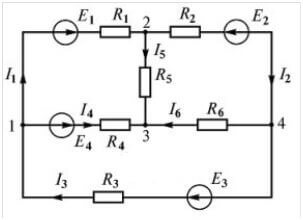
Penseu en un altre circuit:
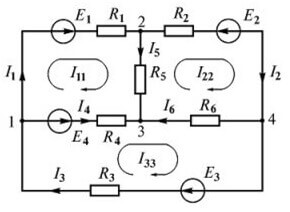
Hi ha fins a quatre fonts d'EMF, però el procediment de càlcul és el mateix, primer escollim la direcció per fer les equacions.
Ara cal fer equacions segons la primera llei de Kirchhoff. Per al primer node (figura 1 a l'esquerra del diagrama):
Jo3 flueix i jo1, Jo4 segueix, d’aquí els signes. Per a la segona:
Per a la tercera:
Pregunta: "Hi ha quatre nodes, i només hi ha tres equacions, per què? ”El fet és que el nombre d'equacions de la primera regla de Kirchhoff és igual a:
Nequacions= nnusos-1
I.e. Només hi ha 1 equacions menys que nodes, perquè això és suficient per descriure els corrents a totes les branques, aconsello una vegada més pujar al circuit i comprovar si tots els corrents estan escrits en les equacions.
Ara passem a la construcció d'equacions segons la segona regla. Per al circuit primari:
Per al segon circuit:
Per al tercer circuit:
Si substituïm els valors de les tensions i resistències reals, resulta que la primera i la segona lleis són justes i es compleixen. Aquests són exemples senzills, a la pràctica s’han de resoldre problemes molt més voluminosos.
Conclusió. El més important a l’hora de calcular amb l’ajuda de la primera i segona lleis Kirchhoff és l’observança de la regla per fer equacions, és a dir. tingueu en compte la direcció del flux de corrent i el bypass del circuit per a la correcta disposició de signes per a cada element del circuit.
Lleis de Kirchhoff per al circuit magnètic
Els càlculs dels circuits magnètics també són importants en l’enginyeria elèctrica, ambdues lleis han trobat la seva aplicació aquí. L’essència segueix sent la mateixa, però el tipus i la mida canvien, mirem aquest tema amb més detall. Primer cal tractar els conceptes.
La força magnetomotriu (MDS) està determinada pel producte del nombre de voltes de la bobina, pel corrent que la travessa:
F = w * i
El voltatge magnètic és el producte de la força i el corrent del camp magnètic a través d'una secció, mesurada a Amperes:
Um= H * I
O flux magnètic mitjançant resistència magnètica:
Um= F * Rm
L és la longitud mitjana de la trama, μr i μ0 - permeabilitat magnètica relativa i absoluta.
Escrivint una analogia, escrivim la primera llei de Kirchhoff per a un circuit magnètic:
És a dir, la suma de tots els fluxos magnètics a través del node és zero. Has notat que això sembla gairebé igual que en un circuit elèctric?
Aleshores la segona llei de Kirchhoff sona a "La suma del MDS al circuit magnètic és igual a la suma UM (tensió magnètica).
El flux magnètic és igual a:
Per a un camp magnètic alternatiu:
Depèn només de la tensió a través del bobinat i no dels paràmetres del circuit magnètic.
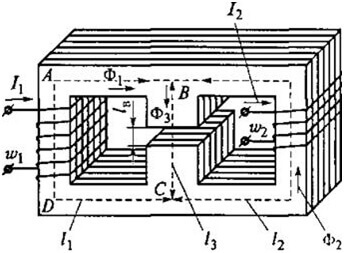
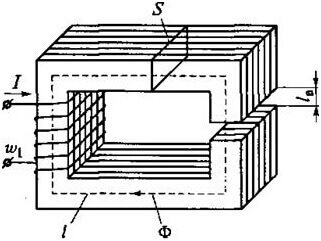
A tall d’exemple, considereu aquest contorn:
Aleshores per a ABCD obtenim la següent fórmula:
En els circuits amb un buit aeri, són certes les relacions següents:
Resistència magnètica:
I la resistència del buit aeri (a la dreta al nucli):
On S és l’àrea principal.
Per comprendre plenament el material i revisar visualment alguns dels matisos d’ús de les regles, us recomanem que us familiaritzeu amb les conferències que s’ofereixen al vídeo:
Els descobriments de Gustav Kirchhoff van contribuir significativament al desenvolupament de la ciència, especialment l’enginyeria elèctrica.Amb la seva ajuda, és força senzill calcular qualsevol circuit elèctric o magnètic, corrents en ell i tensions. Esperem que les regles de Kirchhoff per a circuits elèctrics i magnètics us resultin més clares.
Materials similars:

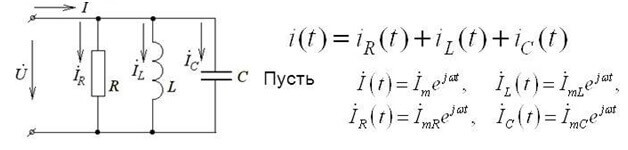
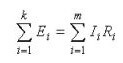
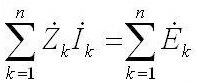
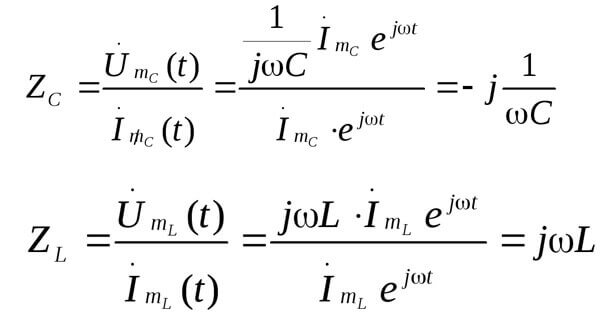

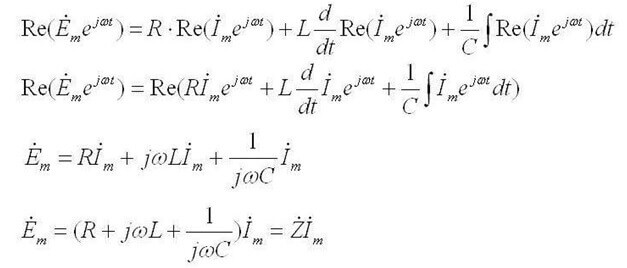
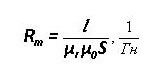
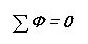
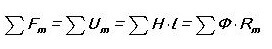
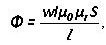
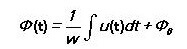
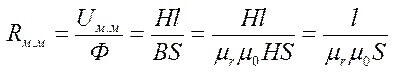
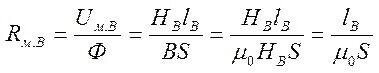


Quan composem ur segons la primera llei de Kirchhoff, és a dir, una bona explicació de la primera ur. Per què no hi ha cap explicació per al segon i el tercer, quan tot és molt més obvi allà? I2 hi flueix clarament, però per alguna raó té un signe positiu
a la tercera equació, de manera que generalment hi flueixen tots tres. Per què són positius?
Tingueu en compte que al principi de l’article l’equació es considera en la forma I1 = I2 + I3, si transferiu tot al costat esquerre de l’equació, I1-I2-I3 = 0. El mateix es va fer allà.
Per al segon node:
I1 = I5 + I2
movent-ho tot en una direcció sortirà:
I1-I5-I2 = 0
Si comparem amb la direcció del bypass del circuit, quedarà clar que és millor canviar els signes, és a dir, multiplicar per menys 1.
Sortirà
-I1 + I5 + I2 = 0
que equival
I2 + I5-I1 = 0